library(tidyverse)6 Exploration von numerischen Daten
- Kernpakete aus
tidyversebenennen - ein Workflow (Daten einlesen, zusammenfassen, darstellen) mit
tidyversedurchführen - Funktionen des Pakets
dplyrfür Datentransformation anwenden
tidyverse ist eine Sammlung von R-Paketen, die explizit für Datenanalyse entwickelt wurden (https://www.tidyverse.org/). tidyverse versucht durch gemeinsame Philosophie in Design, Grammatik und Datenstruktur die Datenanalyse zu erleichtern (https://design.tidyverse.org/). Auch wenn tidyverse auf den ersten Blick etwas fremd erscheint, es ist ein Teil von R, kein eigenes Universum. Es ist also völlig in Ordnung, R-Basisfunktionen mit Funktionen aus tidyverse zu mischen.
Das wichtigste Einführungsbuch zu tidyverse ist sicherlich R4DS: “R for Data Science” (Wickham, Çetinkaya-Rundel, and Grolemund 2023), das Sie kostenlos online lesen können (https://r4ds.had.co.nz/).
6.1 Grundpakete
tidyverse enthält folgende Grundpakete, die alle installiert werden, wenn Sie install.packages('tidyverse') ausführen.
| Paketname | Kurzbeschreibung |
|---|---|
ggplot2 |
Visualisierung |
dplyr |
Datentransformation |
tidyr |
Datenbereinigung |
readr |
Daten einlesen |
purrr |
Funktionale Programmierung (Funktionen auf Objekte anwenden) |
tibble |
Erweiterung von data.frame |
stringr |
Funktionen für Strings, d. h. Textvariablen |
forcats |
Funktionen für factor |
Jedes dieser Pakete hat ein Cheat Sheet, eine übersichtliche Zusammenstellung der Funktionen des Pakets. Sie bekommen die Cheet Sheats über die tidyverse-Seite (https://www.tidyverse.org/packages/), indem Sie auf das jeweilige Paket klicken und zum Abschnitt ‘Cheatsheet’ scrollen.
6.2 Der explorative Workflow
6.2.1 Daten einlesen, revisited
Als Erstes laden wir die Bibliothek tidyverse.
Sie kennen bereits die Funktion read_delim() zum Einlesen von Textdateien. Die Funktion ist die allgemeinste Funktion der read_* Familie aus readr in tidyverse; read_csv() und read_csv2() sind jeweils für Komma- und Strichpunkt-getrennte Datensätze gedacht. In der Basisinstallation von R (also außerhalb von tidyverse) gibt die sehr umfangreiche Funktion read.table(), die ebenfalls zum Einlesen von Textdateien verwendet wird. Man könnte berechtigterweise fragen, warum neue Funktion (read_*) für etwas erfinden, was es schon gibt. Die Autoren von tidyverse versprechen Konsistenz und Geschwindigkeit. Ersteres war schon immer ein Problem von R, da es nicht von Computerspezialisten, sondern von Anwendern erfunden wurde. Daher ist eine Vereinheitlichung durch tidyverse mehr als willkommen. Und Geschwindigkeit ist spätestens bei größeren Datensätzen ein wichtiger Punkt.
Wir sehen uns Daten des Deutschen Wetterdienstes an, die ich am 24. Mai 2020 heruntergeladen habe (https://www.dwd.de/DE/leistungen/klimadatendeutschland/klimadatendeutschland.html). Der Datensatz enthält Stundenwerte für relative Luftfeuchte (%) und Lufttemperatur (°C) von drei Wetterstationen, nämlich Hof, Frankfurt und Köln-Bonn. Die Daten sind in der Datei “Drei_Stationen.csv” gespeichert.
Beim Einlesen zeigt Ihnen read_delim() bereits, welche Spalten und welche Datentypen es erkennt, mit trim_ws = T werden Leerzeichen aus Spalten entfernt, weil die Daten sonst falsch eingelesen werden.
temp_humid <- read_delim('Daten/Drei_Stationen.csv', delim = ';', trim_ws = T)Es sollte für Sie bereits Routine sein, das Ergebnis des Einlesens zu kontrollieren.
temp_humidAlternative können Sie die Funktion glimpse() verwenden.
glimpse(temp_humid)Rows: 39,600
Columns: 6
$ STATIONS_ID <dbl> 2261, 2261, 2261, 2261, 2261, 2261, 2261, 2261, 2261, 2261…
$ MESS_DATUM <dbl> 2018111900, 2018111901, 2018111902, 2018111903, 2018111904…
$ QN_9 <dbl> 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3…
$ TT_TU <dbl> -2.8, -2.5, -2.3, -2.0, -1.9, -2.1, -1.8, -1.5, -1.1, -0.6…
$ RF_TU <dbl> 99, 100, 100, 100, 99, 99, 99, 99, 99, 97, 95, 93, 94, 88,…
$ eor <chr> "eor", "eor", "eor", "eor", "eor", "eor", "eor", "eor", "e…In diesem Datensatz sind folgende Variablen (Spalten) enthalten (s. Datensatzbeschreibung des DWDs)
| Variablen | Beschreibung |
|---|---|
| STATIONS_ID | Stationsidentifikationsnummer |
| MESS_DATUM | Zeitstempel im Format yyyymmddhh |
| QN_9 | Qualitätsniveau der nachfolgenden Spalten |
| TT_TU | Lufttemperatur in 2 m Höhe °C |
| RF_TU | relative Feuchte % |
| eor | Ende data record |
6.3 Geschickter Umgang mit Zeit und Datum
Ein weiteres Paket, das zwar nicht zum Kern von tidyverse gehört, jedoch trotzdem extrem nützlich ist, heißt lubridate. Das haben wir bereits im letzten Kapitel verwendet, um aus einem Datum das Jahr zu extrahieren. lubridate hilft aber auch, Text sehr einfach in richtige Datums-Objekte zu transformieren. Wir transformieren die Spalte temp_humid$MESS_DATUM in ein richtiges Datum mit Uhrzeit. Die Funktion ymd_h() kann character in ein richtiges Datumsformat transformieren, wenn das Datum als year, month, day, hour codiert ist. Es gibt noch weitere Varianten der Codierung, die Sie bei Bedarf in der Hilfe nachschlagen sollten.
library(lubridate)
temp_humid$MESS_DATUM <- ymd_h(temp_humid$MESS_DATUM)
temp_humid6.3.1 Daten zusammenfassen
Die drei Wetterstationen haben folgende IDs:
station_ids <- c('2261' = 'Hof', '1420' = 'Frankfurt', '2667' = 'Koeln')Wir zählen nach, wie viele Messpunkte es pro Station gibt. Die Funktion count() kennen Sie bereits. Sie zählt, wie häufig unterschiedlichen Merkmalsausprägungen vorkommen:
temp_humid %>%
count(STATIONS_ID)Die Zeichenkombination %>% heißt Pipe-Operator (pipe) und wird als ‘und dann’ gelesen (then). Diesen Operator haben wir bereits im letzten Kapitel verwendet. Der Ausdruck temp_humid %>% count(STATIONS_ID) heißt also: nimm das Objekt temp_humid, und zähle dann die Anzahl der verschiedenen Merkmalsausprägungen zusammen. Der Pipe-Operator ist die Kernphilosophie von tidyverse und wird Ihnen überall begegnen. Der Operator stammt aus dem Paket magrittr (https://magrittr.tidyverse.org/). Seine Hauptaufgabe ist es, den Code übersichtlicher und besser lesbar zu machen (vielleicht nicht gleich zu Beginn der Lernkurve, aber schon bald 😎).
6.4 Die Grammatik der Datenmanipulation – dplyr
Die Funktion count() gehört zum Paket dplyr, das für Datentransformationen zuständig ist. Es ist abermals eine Grammatik. Dieses Paket enthält 5 Grundfunktionen (alle nach Verben benannt, damit man gleich weiß, was frau tut 😄):
| Funktion | Bedeutung |
|---|---|
filter() |
Wähle Daten anhand ihrer Werte |
arrange() |
Sortiere Zeilen |
select() |
Wähle Variablen anhand ihrer Namen |
mutate() |
Erstelle neue Variablen als Funktionen vorhandener Variablen |
summarize() |
Fasse Daten zusammen |
Wenn wir nur von einer bestimmten Station die Anzahl der Messwerte wissen möchten, dann filtern wir vorher.
temp_humid %>%
filter(STATIONS_ID == '2667') %>%
count(STATIONS_ID)Beim Filtern läuft eine logische Abfrage. D. h. es wird bei jedem Eintrag in STATION_ID nachgesehen, ob da der Wert 2667 steht. Wenn da 2667 steht, dann gibt == ein TRUE zurück, wenn da etwas anderes steht, dann gibt == ein FALSE zurück. Und die Funktion filter() behält nur die Zeilen, bei denen == ein TRUE zurückgegeben hat.
Weiter wichtige logische und relationale Operatoren finden Sie hier in der Hilfe zu filter(). Hier ein paar einfache Beispiele:
| Operator | Bedeutung |
|---|---|
==/ > / >= |
ist die linke Seite gleich / größer / größer-gleich als die rechte Seite |
!= |
ist die linke Seite ungleich der rechten Seite |
Zudem kann man bei filter() die Anfragen auch kombinieren. Wir wollen z. B. die Stationen Köln und Hof haben. | ist der logische Operator oder. Wenn man also sowohl Köln als auch Hof haben will, sagt man: finde alles, was entweder gleich Köln oder gleich Hof ist.
temp_humid %>%
filter(STATIONS_ID == '2667' | STATIONS_ID == '2261') %>%
count(STATIONS_ID)Das Gleiche erreicht man mit folgendem Code, indem man Frankfurt ausschließt:
temp_humid %>%
filter(STATIONS_ID != '1420') %>%
count(STATIONS_ID)Alternative kann man auch den Operator %in% verwenden. Dieser ist sehr nützlich, wenn man anhand einer einzelnen Variablen filtert, aber unterschiedliche Einträge auswählen möchte (z. B. zwei Messstationen). Es wird bei jeder Zeile in der Variablen STATIONS_ID nun überprüft, ob hier entweder 2667 oder 2261 stehen.
temp_humid %>%
filter(STATIONS_ID %in% c('2667', '2261')) %>%
count(STATIONS_ID)6.4.1 Daten plotten
Wir sehen uns die Daten erst mal an, bevor wir weiter machen. Wir plotten die Temperatur. Weil es sich um Zeitreihen handelt, kommt auf die \(x\)-Achse die Zeit.
ggplot(data = temp_humid, aes(x = MESS_DATUM, y = TT_TU, color = as_factor(STATIONS_ID))) +
geom_line() +
labs(x = 'Zeit', y = 'Temperatur (°C)', color = 'Stationen')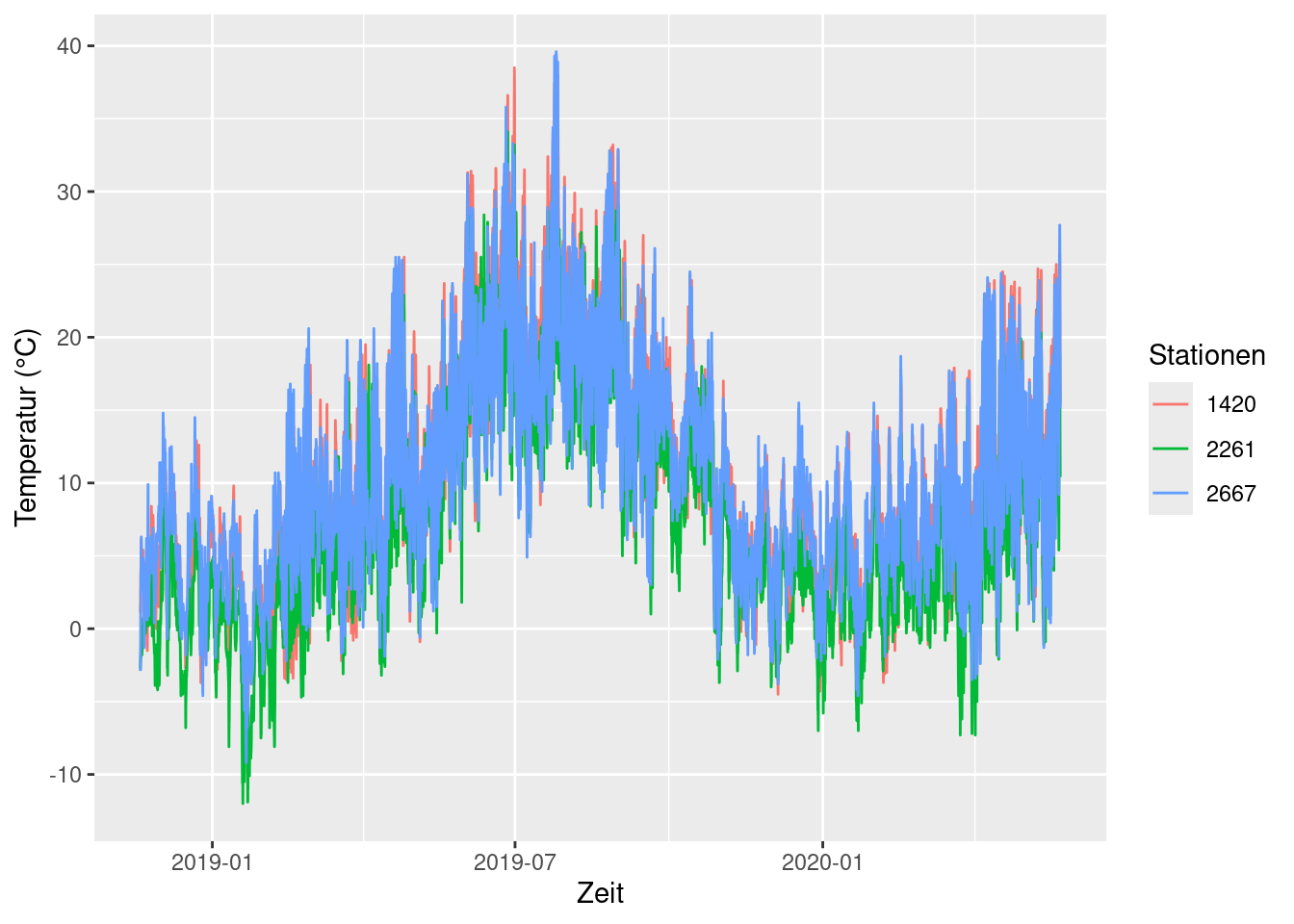
Beachten Sie, dass wir die Variable zum Einfärben, nämlichSTATIONS_ID, direkt in ggplot() in eine kategoriale Variable umgewandelt haben. Sonst werden die Farben als Farbverlauf statt drei unterschiedliche Farben, dargestellt.
Da man erwarten kann, dass sich der Temperaturverlauf innerhalb Deutschlands nicht so stark unterscheidet, überdecken sich die Zeitreihen. Das ist für die Darstellung ungünstig. Daher wäre es besser, wenn wir die Zeitreihen in getrennte Grafiken je Station plotten würden. Dafür gibt es eine neue Funktion aus dem Paket ggplot2, nämlich facet_wrap(). Sie kann eine Grafik mithilfe einer kategorialen Variablen in Teilgrafiken aufteilen.
ggplot(data = temp_humid, aes(x = MESS_DATUM, y = TT_TU)) +
geom_line() +
facet_wrap(~STATIONS_ID, nrow = 3) +
labs(x = 'Zeit', y = 'Temperatur (°C)')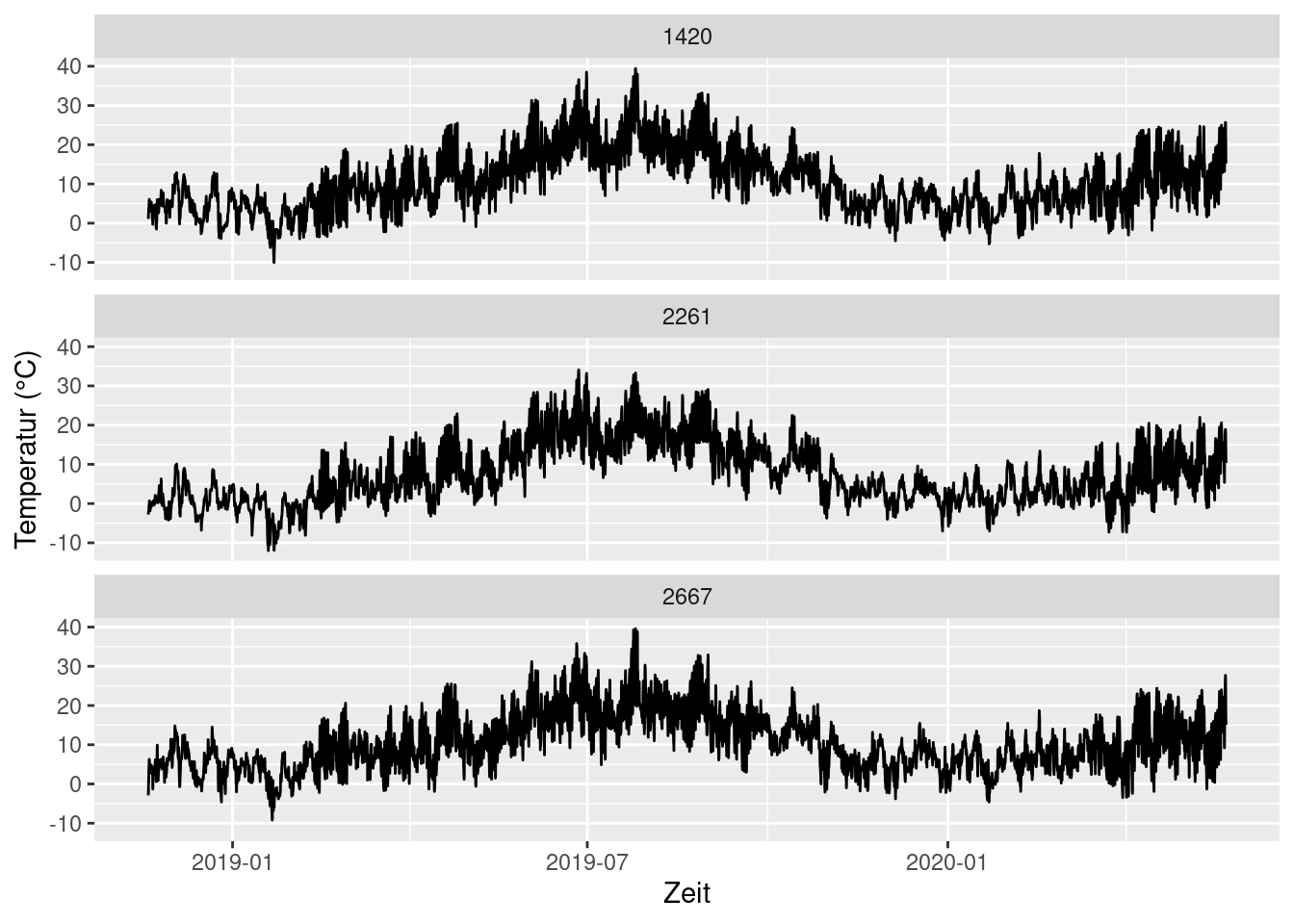
Da wir die Teilgrafiken untereinander darstellen möchten, setzen wir bei facet_wrap() den Parameter nrow = 3. Bei Teilgrafiken kann man auf die Färbung der Zeitreihen verzichten.
6.4.2 Jahresdurchschnittstemperatur
Wie hoch war die Jahresdurchschnittstemperatur auf den drei Stationen? Um diese Frage zu beantworten, erstellen wir zunächst eine neue Variable mit dem Jahr der Messungen. Das kennen Sie bereits aus dem letzten Kapitel. Die Funktion year() gehört zur Bibliothek lubridate. Die Funktion mutate() erstellt die neue Spalte und hängt sie an das Ende des Dataframes.
temp_humid <- temp_humid %>%
mutate(year = year(MESS_DATUM))Da wir die Durchschnittstemperatur für jede Station und jedes Jahr separat berechnen wollen, müssen wir unseren Datensatz nach den Stationen gruppieren. Durch die Gruppierung entstehen intern Gruppen, für die Berechnungen getrennt laufen werden. An den Daten selbst ändert sich nichts.
Als zweiten Schritt nutzen wir dann die Funktion summerise(), die verschiedene statistische Zusammenfassungen der Daten berechnen kann. In diesem Fall möchten wir mithilfe der Funktion mean() den Mittelwert berechnen. Wir nennen den neu berechneten Datensatz yearly_means.
yearly_means <- temp_humid %>%
group_by(STATIONS_ID, year) %>%
summarize(mean_T = mean(TT_TU))Wir erhalten einen Datensatz, der pro Jahr und Station einen Mittelwert der Temperatur enthält. Die Variable, die die mittlere Temperatur enthält, haben wir mean_T genannt. Sie steht in der Zeile summarize(mean_T = mean(TT_TU)) links vom Aufruf der Funktion mean(). Der Code mean(TT_TU) berechnet den Mittelwert der Variablen TT_TU, also der Temperatur.
yearly_meansDie Berechnung der Jahresmittelwerte ist sehr kritisch zu sehen. Nicht alle berechneten Werte ergeben Sinn. Diskutieren Sie in der Hausaufgabe warum.
6.4.3 Monatliche Durchschnittstemperatur und ihre Variabilität
Wie hoch war die monatliche Durchschnittstemperatur auf den verschiedenen Stationen und wie stark schwankte sie? Diese Frage können wir beantworten, indem wir Mittelwerte und Standardabweichungen für jeden Monat eines jeden Jahres und jede Station berechnen. Für die Berechnung erstellen wir eine weite Spalte mit dem Monat. Die Funktion month() gehört ebenfalls zur Bibliothek lubridate und extrahiert den Monat aus MESS_DATUM.
temp_humid <- temp_humid %>%
mutate(month = month(MESS_DATUM))
temp_humidJetzt können wir die Mittelwerte und die Standardabweichungen mit der Funktion summarise() berechnen. Diese Funktion kann gleichzeitig verschiedene statistische Zusammenfassungen berechnen. Den Mittelwert berechnen wir erneut mit der Funktion mean() und die Standardabweichung mit der Funktion sd().
Für die Berechnung gruppieren wir die Daten nach STATIONS_ID, year und month mit der Funktion group_by(). Die Mittelwerte sollen ja je Station, Jahr und Monat berechnet werden. Beim Gruppieren gibt man die Variablennamen ohne Anführungszeichen durch Kommas getrennt an. Man kann nach einer oder mehreren Variablen gruppieren, die Logik bleibt immer die gleiche, nämlich group_by(VARIABLE_1) fürs Gruppieren mit einer Variablen oder group_by(VARIABLE_1, VARIABLE_2, VARIABLE_3) für z. B. gruppieren nach drei Variablen.
monthly_means <- temp_humid %>%
group_by(STATIONS_ID, year, month) %>%
summarize(mean_T = mean(TT_TU), sd_T = sd(TT_TU))
monthly_meansDie Variable, die die Standardabweichung enthält, haben wir sd_T genannt.
Das Dataframe monthly_means ist ein gruppiertes tibble. Das ist für die meisten Anwendungen nicht von Belang. Insbesondere ändert es nicht die Daten selbst, sondern nur die interne Organisation des tibble. Manchmal stört die Gruppierung jedoch beim Rechnen mit dem Datensatz und wir lösen sie wieder auf.
monthly_means <- ungroup(monthly_means)Um die monatlichen Daten als Zeitreihen zu plotten, benötigen wir noch eine Variable mit dem dazugehörigen Datum. Die Funktion parse_date_time() kann aus character richtige Datums- und Zeitobjekte erstellen. Sie ist allgemeiner als die oben verwendete ymd_h() Funktion, da man hier das Format explizit angeben kann. In unserem Fall ist das Format ‘ym’ für Jahr und Monat.
monthly_means <- monthly_means %>%
mutate(year_month = parse_date_time(paste0(year, month), orders = 'ym', tz = 'CET'))
monthly_meansDer Code paste0(year, month) “klebt” die Daten in der Variablen year und month zusammen. Das ist nötig, da die Funktion parse_date_time() einen zusammenhängenden Text als Input erwartet und keine zwei getrennten Spalten. Da das Datum außer dem Jahr und dem Monat noch einen Tag benötigt, hat parse_date_time() automatisch den Ersten eines jeden Monats genommen. Beim Erstellen von korrekten Zeitangaben kommt es auch auf die Zeitzone an. Wir sind in Deutschland, da gilt die mitteleuropäische Zeit (engl. central European time, CET). Die Zeitzone ist für unsere Daten zwar nicht wirklich relevant, da wir hier Monatsdaten darstellen. Ich würde sie aber trotzdem richtig setzen, da die Standardeinstellung der Funktion parse_date_time(tz = "UTC") lautet und für Deutschland falsch ist.
ggplot(data = monthly_means, aes(x = year_month, y = mean_T, col = factor(STATIONS_ID))) +
geom_line() +
labs(x = 'Zeit', y = 'Temperatur (°C)', color = 'Messstation')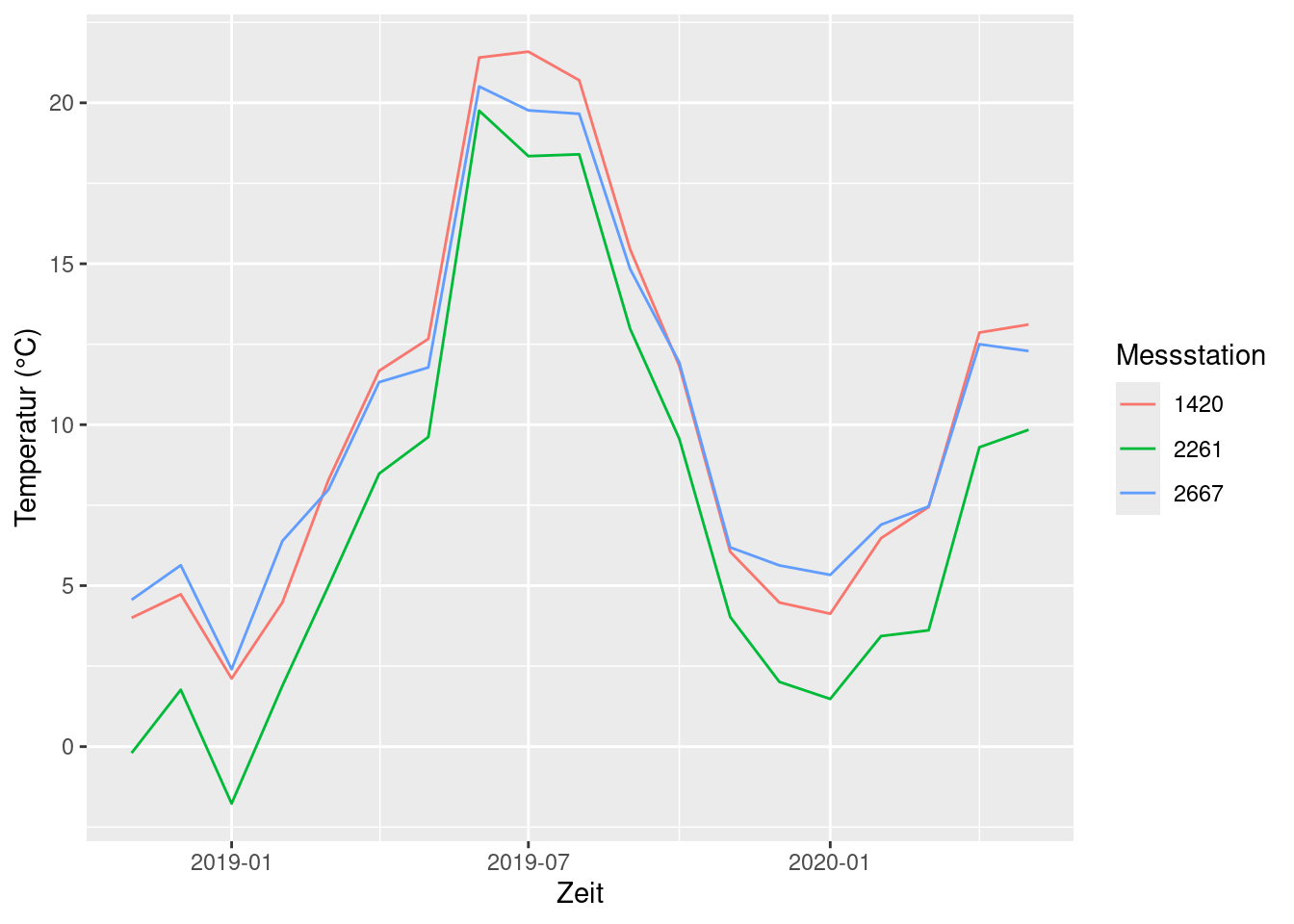
Alternativ können wir die Mittelwerte mit den Standardabweichungen darstellen.
ggplot(monthly_means, aes(x = year_month, y = mean_T, ymin = mean_T - sd_T, ymax = mean_T + sd_T)) +
geom_errorbar() +
geom_point() +
facet_wrap(~STATIONS_ID, nrow = 3) +
labs(x = 'Zeit', y = 'Temperatur (°C)')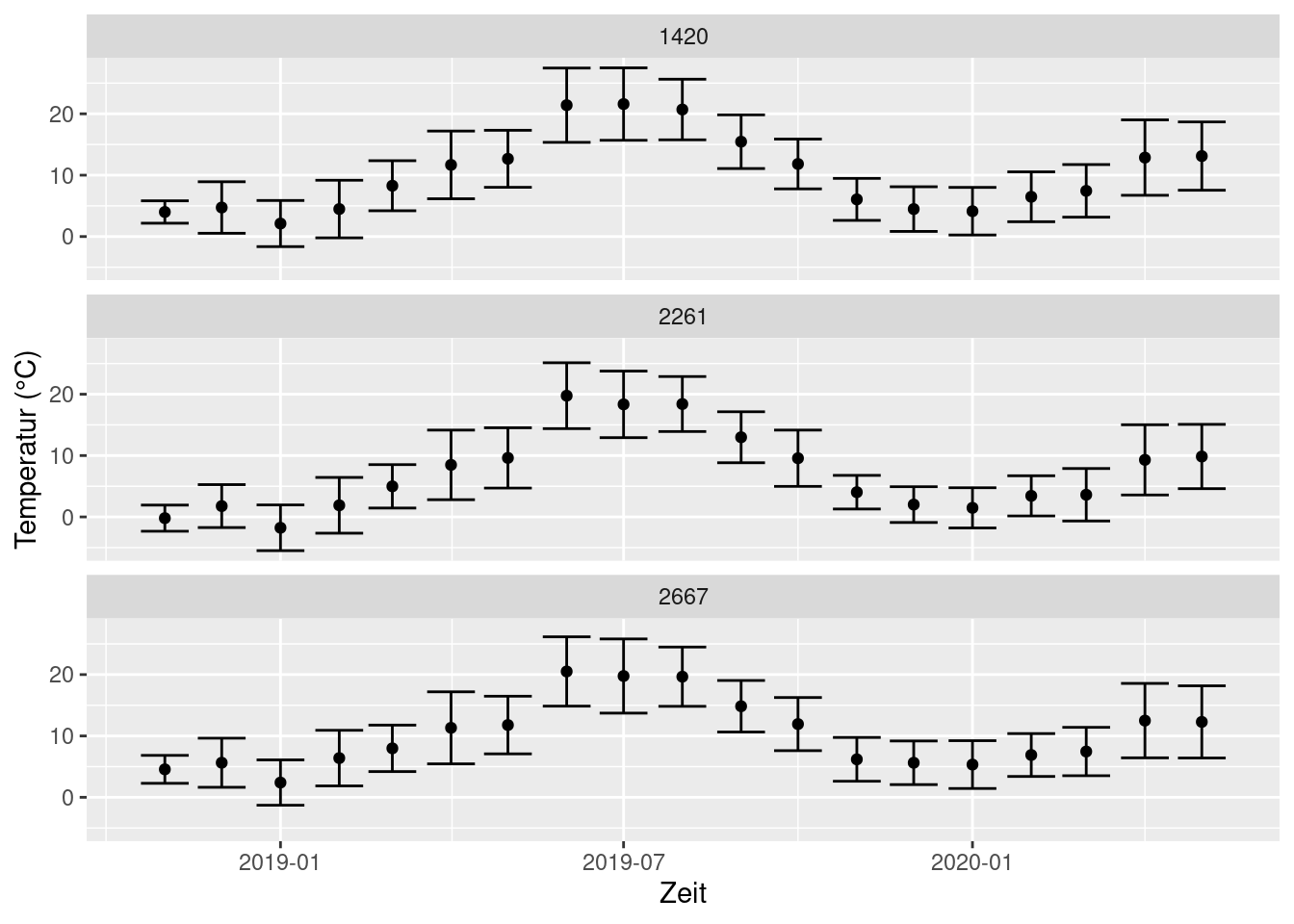
Oder, weil es gerade Spaß macht, als halb-transparentes Band 😎.
ggplot(monthly_means, aes(x = year_month, y = mean_T, ymin = mean_T - sd_T, ymax = mean_T + sd_T)) +
geom_ribbon(alpha = 0.5) +
geom_line() +
facet_wrap(~STATIONS_ID, nrow = 3) +
labs(x = 'Zeit', y = 'Temperatur (°C)')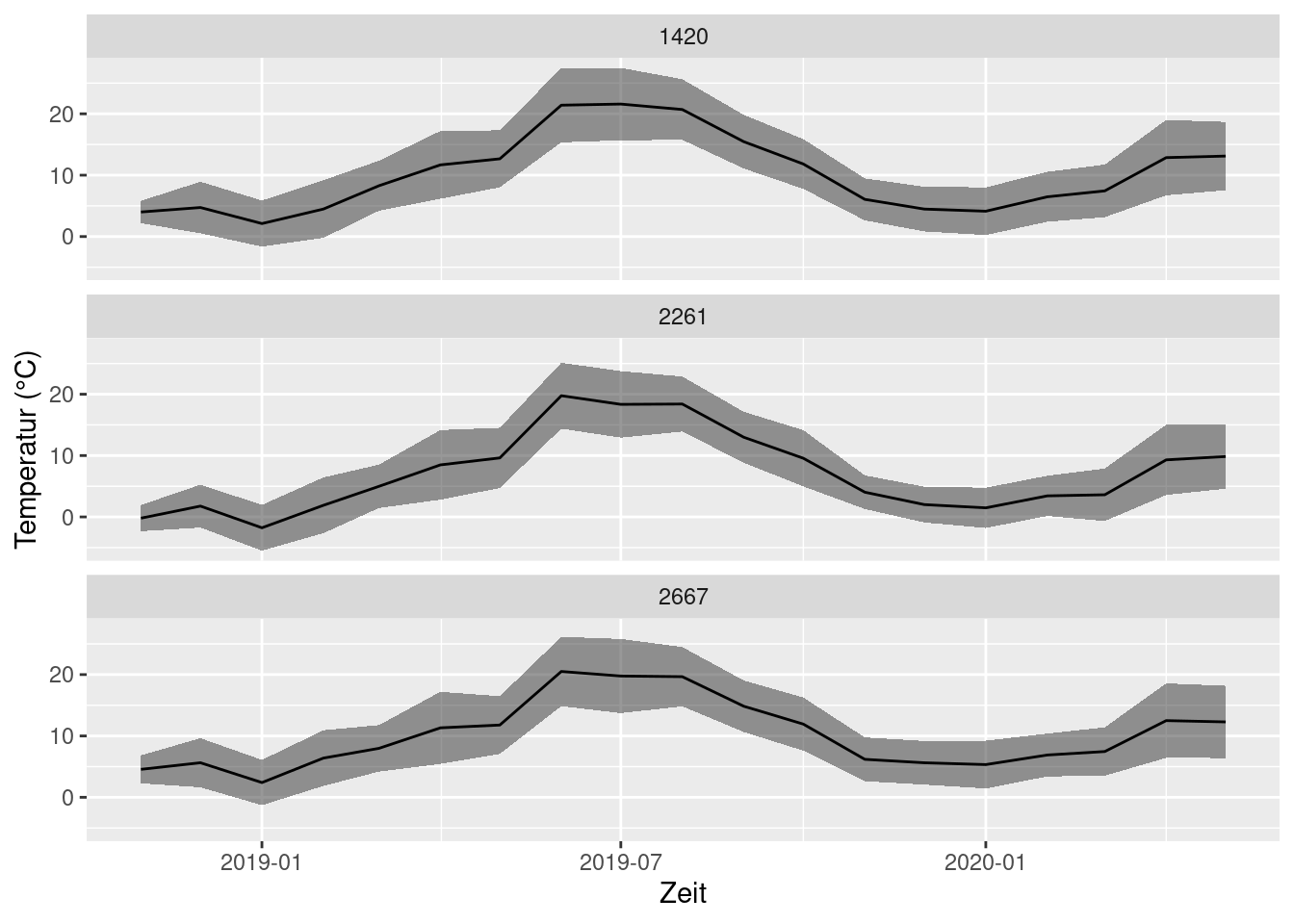
Ein letzter Trick. Die Überschriften für die Teilgrafiken sind ungeschickt, da man die IDs als Mensch einfach nicht zuordnen kann. Weiter oben haben wir einen benannten Vektor definiert, der die Klarnamen enthält.
station_ids 2261 1420 2667
"Hof" "Frankfurt" "Koeln" Diesen Vektor nutzen wir als Titel.
ggplot(monthly_means, aes(x = year_month, y = mean_T, ymin = mean_T - sd_T, ymax = mean_T + sd_T)) +
geom_ribbon(alpha = 0.5) +
geom_line() +
facet_wrap(~STATIONS_ID, nrow = 3, labeller = labeller(STATIONS_ID = station_ids)) +
labs(x = 'Zeit', y = 'Temperatur (°C)')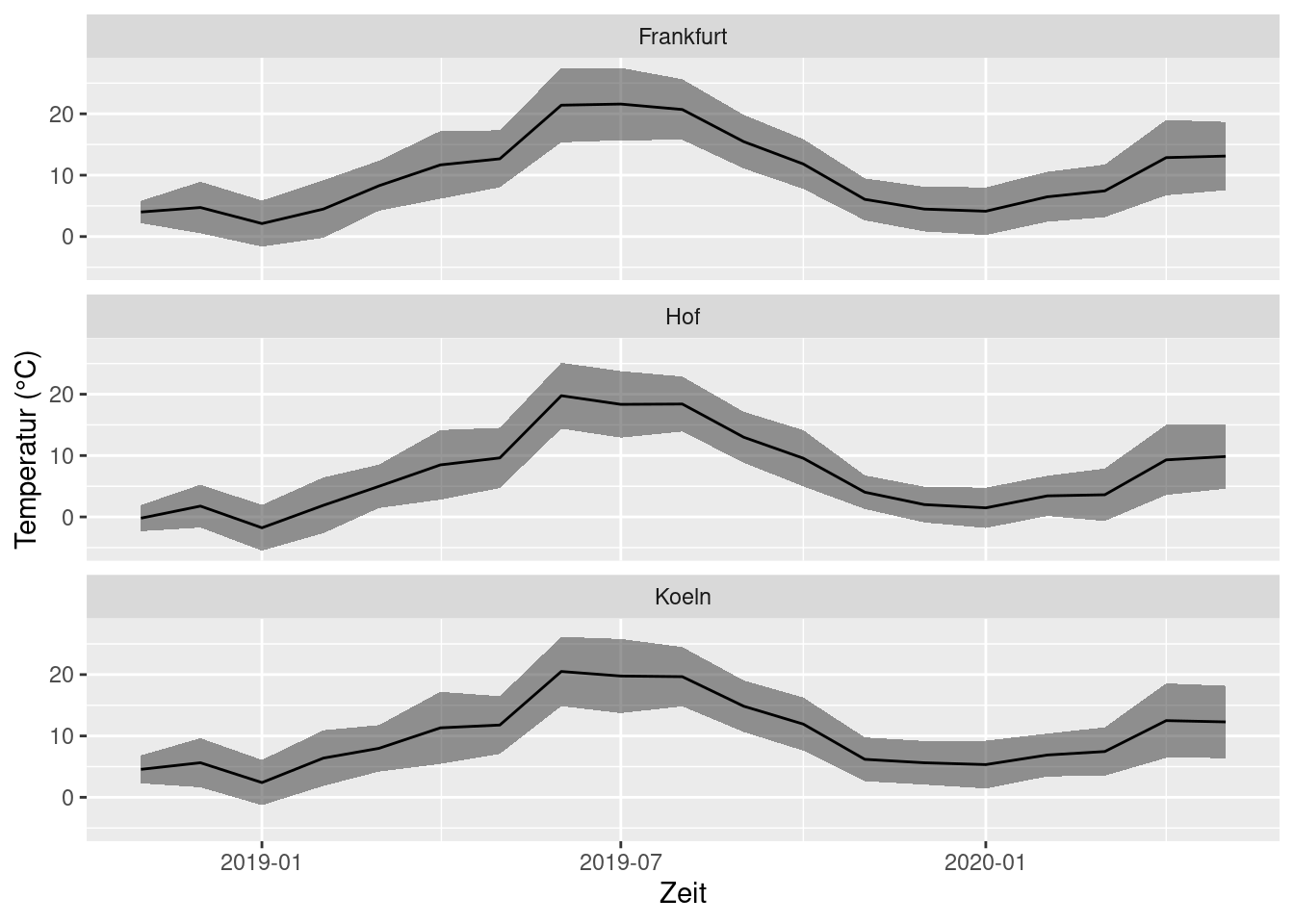
6.5 Weiterführende Literatur und Videos
R4DS Wickham, Çetinkaya-Rundel, and Grolemund (2023): Kapitel 3 “Data transformation”
Eine live Analyse des Hauptautors von
tidyverse, Hadley Wickham. Empfehlenswert, auch wenn er viel zu schnell tippt 😄.
6.6 Hausaufgaben
6.6.1 Was bedeutet der Code?
Was bedeuten die Parameter ymin und ymax im folgenden Code?
ggplot(monthly_means, aes(x = year_month, y = mean_T, ymin = mean_T - sd_T, ymax = mean_T + sd_T))6.6.2 Welche Mittelwerte sind sinnvoll?
Diskutieren Sie kritisch, für welche Zeitabschnitte in unseren Daten die Berechnung der Jahresmitteltemperatur sinnvoll ist und interpretiert werden kann. Begründen Sie. Die Besprechung erfolgt in der nächsten Übung.
6.6.3 Lab 02: Pünktlichkeit von Flügen
Bearbeiten Sie das Lab 02. Die Besprechung erfolgt in der nächsten Übung.
6.7 Ihre Arbeit einreichen
Reichen Sie die Aufgabe Kapitel 6.6.1 bei fiete.ai ein und erhalten Sie feedback: