set.seed(123)
pop_size <- 12000
student_id <- 1:pop_size
anreise <- c(runif(n = pop_size * 0.8, min = 5, max = 40),
runif(n = pop_size * 0.2, min = 60, max = 120))
geschlecht <- sample(c('m', 'w', 'd'), size = pop_size, replace = TRUE)
studienordnung <- sample(c('alt', 'neu'), size = pop_size, replace = TRUE)
wohnort <- sapply(anreise, function(x) {
if(x < 30) 'stadt'
else 'land'
})
studiendauer <- rnorm(n = pop_size, mean = 3.5, sd = 0.6)8 Hypothesentests mit Randomisierung
- Idee hinter randomisierten Tests erklären.
- Tests mit dem Paket
inferdurchführen.
8.1 Studiendauer in Werdeschlau
Wir beschäftigen uns mit einem fiktiven Beispiel.
An der (kleinen) Universität Werdeschlau möchte man wissen, ob die vor einiger Zeit eingeführte Studienordnung die Studiendauer verändert hat. Dazu werden 300 Studierende zufällig über die Dauer ihres Studiums befragt. Zusätzlich werden noch andere Daten erhoben, aber mit diesen beschäftigen wir uns in einer anderen Übung.
8.1.1 Simulation der Grundgesamtheit
Bei statistischer Inferenz geht es unter anderem darum, die Begriffe Zufall und Variabilität zu quantifizieren. Um diese Konzepte zu verstehen, helfen Computerexperimente. Dafür erstellen wir uns unsere eigene Grundgesamtheit aller Studierenden an der Universität Werdeschlau. Das hat den Vorteil, dass wir viele verschiedene Befragungen durchführen können, die Variabilität der Antworten analysieren und dabei immer mit den wahren Parametern der Grundgesamtheit vergleichen können.
Wir erstellen zunächst die Grundgesamtheit. Die Zeile set.seed(123) sorgt für reproduzierbare Ergebnisse.
Wir setzen geschlecht, wohnort, studiendauer, studienordnung und anreise zu einer Datenmatrix (tibble) zusammen und nennen das Objekt grundgesamtheit.
grundgesamtheit <- tibble(student_id, geschlecht, wohnort, studiendauer, studienordnung, anreise)8.1.2 Befragung simulieren
In der Realität werden natürlich nicht alle 12000 Studierende befragt (wer hat schon so viele Kapazitäten?), sondern eine zufällige Stichprobe erhoben, also eine Teilmenge der Grundgesamtheit.
Um unsere Stichprobe zu erstellen, ziehen wir 300 Studierende ohne Zurücklegen aus unserer Grundgesamtheit. Das entspricht einer einmaligen Befragung von 300 zufällig ausgewählten Studierenden.
set.seed(345)
befragung_size <- 300
befragung <- rep_sample_n(grundgesamtheit, size = befragung_size, replace = FALSE, reps = 1)Wir berechnen den Mittelwert der Studiendauer, jeweils für die alte und neue Studienordnung.
stat_obs <- befragung %>%
group_by(studienordnung) %>%
summarise(dauer = mean(studiendauer))
stat_obsWie groß ist die Differenz der Mittelwerte?
stat_obs$dauer[1] - stat_obs$dauer[2][1] -0.08012473Wie verändert sich die Differenz, wenn wir zufälligerweise andere Studierende befragt hätten? Wir wählen neue Studierende aus und wiederholen die Berechnung des Mittelwerts der Studiendauer.
set.seed(987)
befragung <- rep_sample_n(grundgesamtheit, size = befragung_size, replace = FALSE, reps = 1)
stat_obs <- befragung %>%
group_by(studienordnung) %>%
summarise(dauer = mean(studiendauer))
stat_obsFür diese Gruppe der Befragten beträgt die Differenz der Mittelwerte -0.0547357.
8.2 Workflow in infer
Das Paket infer bietet ein einheitliches Framework für Hypothesentests (Abbildung 8.1). Es hat 4 Verben, die den oben beschriebenen Prozess der Hypothesentests vereinheitlichen und ein Verb für die Visualisierung der Ergebnisse:
specify()Variablen festlegenhypothesize()Nullhypothese definierengenerate()Daten unter der Nullhypothese generierencalculate()Stichprobenverteilung (d.h. Verteilung der Teststatistik) berechnenvisualize()Stichprobenverteilung darstellen
Mit get_p_value kann man den \(p\)-Wert berechnen und mit shade_p_value diesen darstellen lassen.

8.3 Hypothesentest durchführen
8.3.1 Schritt 1: Nullhypothese und Alternativhypothese festlegen
Unsere Forschungsfrage lautet: Hat sich die Studiendauer durch die Einführung der neuen Studienordnung verändert? Daraus ergeben sich folgende Hypothesen:
Nullhypothese H\(_0\): Die Studiendauer hat sich durch die Einführung der neuen Studienordnung nicht verändert. Sie ist gleich geblieben.
Alternativhypothese H\(_A\): Die Studiendauer hat sich durch die Einführung der neuen Studienordnung verändert.
Die Alternativhypothese ist unsere eigentliche Forschungsfrage. Da wir nicht wissen, in welche Richtung die Änderungen erfolgt sein könnte (Verlängerung oder Verkürzung der Studiendauer), formulieren wir eine sogenannte beidseitige Alternativhypothese. Beidseitig heißt, dass Änderungen in beide Richtungen interessant sind.
Wir berechnen zunächst die tatsächlich in den Daten (der Befragung) beobachtete Differenz zwischen den Studiendauern nach der alten und der neuen Studienordnung, also unsere Teststatistik. Die Differenz wird als alt \(-\) neu berechnet. Die Funktion observe() im Paket infer berechnet diese Teststatistik.
d_hat <- befragung %>%
observe(formula = studiendauer ~ studienordnung,
stat = "diff in means",
order = c('alt', 'neu'))
d_hat8.3.2 Schritt 2: Simulationsexperimente durchführen
Um Daten unter der Nullhypothese, d. h. wenn die Nullhypothese gilt, zu produzieren, permutieren wir 10000 Mal die Variable studienordnung. Denn, wenn die Studiendauer nicht von der Studienordnung abhängt, dann sind diese beiden Variablen unabhängig. Das legt die Zeile hypothesize(null = "independence") fest. Damit wir alle dieselben Ergebnisse bekommen, setzen wir erneut set.seed().
set.seed(56)
null_dist <- befragung %>%
specify(studiendauer ~ studienordnung) %>%
hypothesize(null = "independence") %>%
generate(reps = 10000, type = "permute") %>%
calculate(stat = "diff in means", order = c('alt', 'neu'))8.3.3 Schritt 3: Ergebnisse darstellen
Wir stellen die Verteilung der Teststatistiken unter der Nullhypothese als ein Histogramm dar und zeichnen zusätzlich ein, wo sich die beobachtete Teststatistik (d. h. der beobachtete Unterschied der Mittelwerte) befindet als vertikale rote Linie. Die schattierten Bereiche zeigen Teststatistiken aus den Permutationen, die so extrem oder noch extremer sind, als die beobachtete Teststatistik von -0.0547357. Da unsere Alternativhypothese lautet, dass sich die Studiendauer verändert hat, betrachten wir extreme Werte sowohl bei der Verlängerung als auch bei der Verkürzung der Studiendauer als Evidenz gegen die Nullhypothese und zugunsten der Alternativhypothese. Daher färben wird die Bereiche links und spiegelbildlich rechts der beobachteten Teststatistik ein.
visualize(null_dist) +
shade_p_value(obs_stat = d_hat, direction = "two-sided")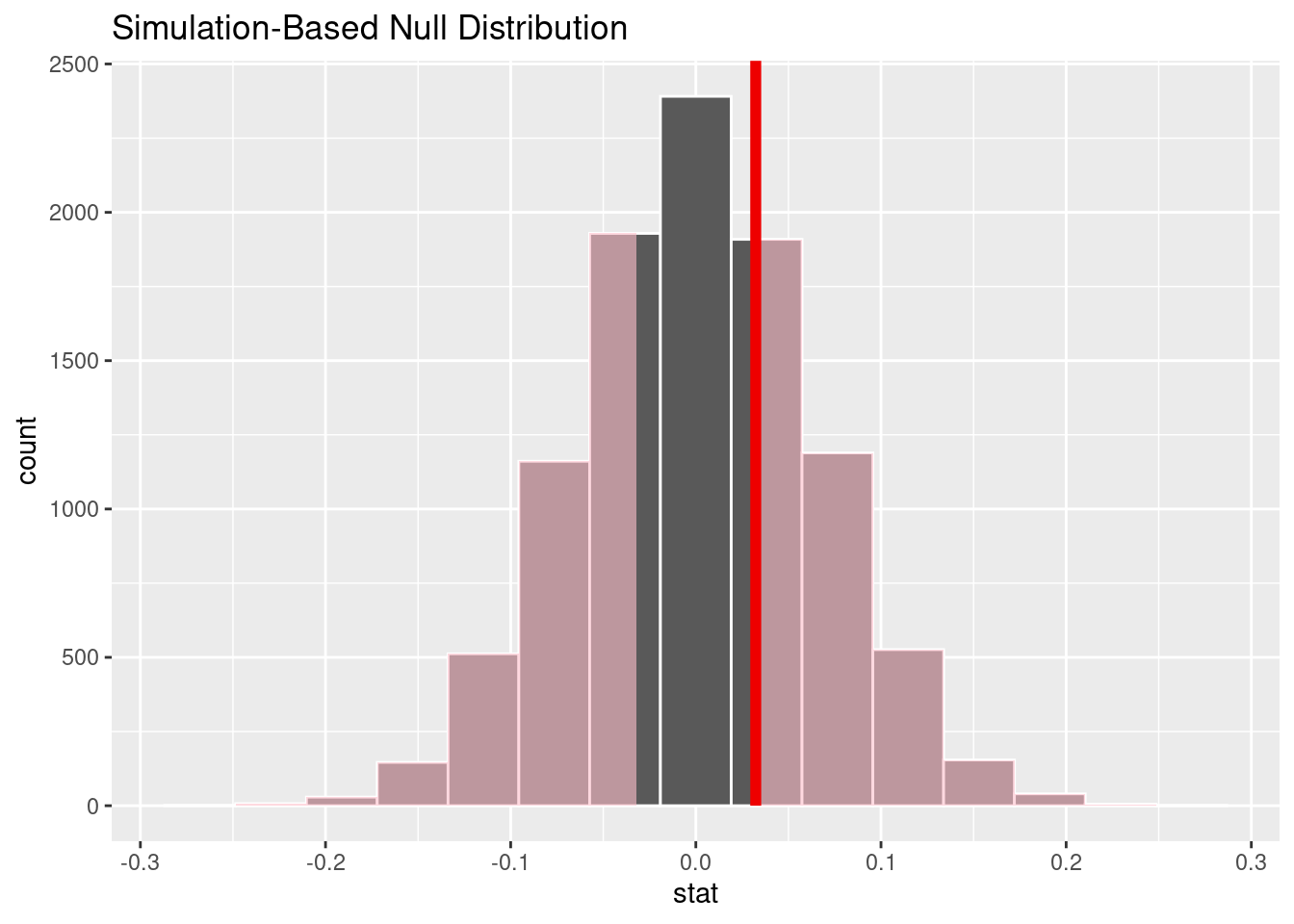
8.3.4 Schritt 4: \(p\)-Wert berechnen und Schlussfolgerungen ziehen
Der folgende Code berechnet den \(p\)-Wert. Der \(p\)-Wert gibt uns die Wahrscheinlichkeit an, eine Teststatistik (also die Differenz der Mittelwerte) so extrem oder noch extremer als -0.0547357 zu beobachten, wenn die Nullhypothese tatsächlich korrekt ist. In anderen Worten, wenn wir in infer Daten generieren unter der Nullhypothese (d. h. übereinstimmend mit der Nullhypothese), dann kommt eine Differenz von -0.0547357 oder noch größer und spiegelbildlich von 0.0547357 oder noch kleiner, mit einer Wahrscheinlichkeit von \(p\) vor. Um den \(p\)-Wert zu berechnen, rechnen wir den Anteil der eingefärbten Bereiche aus.
null_dist %>%
get_p_value(obs_stat = d_hat, direction = "two-sided")Wir sehen also, dass Differenzen zwischen den Mittelwerten von -0.0547357 oder noch größer und spiegelbildlich von 0.0547357 oder noch kleiner in 39.58% der Fälle vorkommen, wenn die Nullhypothese gilt. Eine solche Differenz ist also nichts Besonderes. Unser Signifikanzniveau ist \(\alpha = 0.05\). Da \(p > \alpha\), behalten wir die Nullhypothese bei. Es gibt also keinen Unterschied in der Studiendauer zwischen der alten und der neuen Studienordnung.
8.4 Aufgaben
8.4.1 Vertiefung des Themas Zufall und Variabilität
Arbeiten Sie das Tutorium Foundations of inference: 1 - Sampling Variability durch.