Kapitel 8 Bootstrapping und Konfidenzintervalle
- Funktionsweise von Bootstrap erklären
- Bootstrap-Konfidenzintervalle für Mittelwert berechnen
Im Kapitel 7 haben Sie gesehen, dass Statistiken aus zufällig gezogenen Stichproben, dem Zufall unterliegen. Sie sind Zufallsvariablen. Diesen Zufall haben wir mithilfe der Stichprobenverteilung dieser Statistiken quantifiziert, in dem wir den Standardfehler, die Standardabweichung aus der Stichprobenverteilung, berechnet haben.
Die Statistik, die wir im Kapitel 7 berechnet haben, war der Anteil von Studierenden, die entweder in der Stadt oder auf dem Land wohnen. Mit jeder Stichprobe, aus der wir diesen Anteil berechnet haben, haben wir eigentlich geschätzt, wie groß der wahre Anteil der Stadt- und Landbewohner in der Grundgesamtheit (allen 12000 Studierenden von Werdeschlau) ist. Der aus der Stichprobe berechnete Anteil ist also ein Schätzer für den wahren Anteil in der Grundgesamtheit. Dieser Schätzer ist eine Zufallsvariable (s.o.) und wie jede andere Zufallsvariable ist er durch seine Verteilung, nämlich die Stichprobenverteilung charakterisiert.
Wir können jetzt also eine Menge statistischer Begriffe mithilfe unseres Beispiels mit Leben füllen:
- Grundgesamtheit: alle Studierenden der Universität Werdeschlau
- zufällige Stichprobe: eine zufällig ausgesuchte Gruppe von Studierenden
- Parameter der Grundgesamtheit: z.B. der wahre Anteil von Studierenden, die in der Stadt oder auf dem Land leben
- Schätzer für diesen Parameter der Grundgesamtheit: Anteil der Studierenden, die in der Stadt oder auf dem Land leben, berechnet aus der zufälligen Stichprobe. Da die Stichprobe zufällig ist, kann man davon ausgehen, dass sie repräsentativ für die Grundgesamtheit ist und der Schätzer unverzerrt (unbiased, d.h. ohne einen systematischen Fehler).
- Inferenz: schließen auf die Grundgesamtheit darf man, wenn die Stichprobe zufällig erhoben wurde und repräsentativ für die Fragestellung ist.
Die Begriffe Statistik, Schätzer, Schätzfunktion und Stichprobenfunktion werden als Synonyme verwendet. Die Statistik ist ja auch eine Funktion, da sie mit einer Formel eine Zahl aus Daten (Stichprobe) berechnet. Sie fasst die Stichprobe also zusammen.
Im echten Leben werden Sie kaum wiederholt befragen (Stichproben ziehen) können. Das ist vollkommen unrealistisch und nur für Computerexperimente ein tolles Werkzeug. In diesem Kapitel wird es darum gehen, wie man nun im richtigen Leben mit einer Stichprobe einen Parameter der Grundgesamtheit schätzen kann und dabei seine Variabilität quantifiziert.
8.1 Bootstrapping, die Münchhausenmethode
Wenn wir nur eine Stichprobe haben, werden wir den Parameter der Grundgesamtheit daraus schätzen. Der Schätzer kann der Mittelwert oder eben auch der Anteil sein, so wie bei unseren vorherigen Beispielen mit dem Mittelwert der Anreisezeit oder dem Anteil der Studierenden aus der Stadt bzw. vom Land.
Da jede Stichprobe dem Zufall unterliegt und der Schätzer somit eine Zufallsvariable darstellt, würden wir gerne wissen, wie gut wir schätzen.
Gibt es einen plausiblen Bereich für den Mittelwert der Anreisezeit? Plausibel meint, dass wenn wir sehr oft verschiedene zufällige Stichprobe ziehen, dieser Bereich in sagen wir mal 95% der Fälle den wahren Mittelwert einschließt. Solche Plausibilitätsbereiche nennt man Konfidenzintervalle.
Es gibt mehrere Methoden, solche Konfidenzintervalle zu berechnen. Wenn man die Verteilung des Schätzers kennt, wie beim Mittelwert (Normalverteilung), dann kann man daraus den Standardfehler berechnen (nennen wir diesen \(SE\)). Ein 95%-Konfidenzintervall wäre dann \(\hat{\mu} \pm 1.96 \cdot SE\), wobei \(\hat{\mu}\) der geschätzte Mittelwert ist. Das Hütchen steht für geschätzt. Diese Formel haben Sie bestimmt schon in der Grundvorlesung Statistik gesehen.
Es gibt aber Schätzer, für die keine theoretische Verteilung bekannt ist. Da muss man eine andere Methode anwenden. Eine bekannte Methode heißt Bootstrapping (Bootstrap-Verfahren), manchmal auch Münchhausenmethode. Sie klingt auf den ersten Blick wie ein Selbstbetrug, so als ob man sich selbst an den Haaren aus dem Sumpf zieht (Abblildung 8.1), hat aber fundierte mathematische Wurzeln. Bootstrap wurde von Efron (1979) Ende der 70er vorgestellt und hat sich seitdem als eine der wichtigsten Resampling-Strategien etabliert.
](figures/M%C3%BCnchhausen-Sumpf-Hosemann.png)
Abbildung 8.1: Münchhausen zieht sich aus dem Sumpf (Theodor Hosemann (1807-1875), Public domain, via Wikimedia Commons), Link zum Bild
Das Prinzip beim Bootstrap ist, dass die Stichprobe die Rolle der Grundgesamtheit übernimmt. Abbildung 8.2 zeigt das Vorgehen aus dem Kapitel 7. Wir ziehen mehrere echte Stichproben aus einer Grundgesamtheit, erhalten eine Stichprobenverteilung und können den Parameter der Grundgesamtheit schätzen.
![Berechnen einer Stichprobenverteilung durch wiederholtes Stichproben ziehen. Abbildung aus [@Hesterberg2015], dort Figure 4. Die Publikation ist open-access und darf für nicht-kommerzielle Zwecke verwendet werden. [Link zur Lizenz](https://www.tandfonline.com/action/showCopyRight?scroll=top&doi=10.1080%2F00031305.2015.1089789)](figures/sampling_world.png)
Abbildung 8.2: Berechnen einer Stichprobenverteilung durch wiederholtes Stichproben ziehen. Abbildung aus (Hesterberg 2015), dort Figure 4. Die Publikation ist open-access und darf für nicht-kommerzielle Zwecke verwendet werden. Link zur Lizenz
In Abbildung 8.3 haben wir nur eine Stichprobe. Wir gehen davon aus, dass diese Stichprobe eine Miniatur der Grundgesamtheit ist, also zufällig gezogen wurde und repräsentative ist. Mit dieser Grundidee im Kopf, ersetzten wir die Grundgesamtheit durch diese Stichprobe und verfahren (fast) genauso, um die Stichprobenverteilung zu ermitteln. Der einzige Unterschied ist, dass wir aus dieser einen Stichprobe mit Zurücklegen neue Stichproben (Bootstrap-Stichproben) ziehen.
![Berechnen einer Stichprobenverteilung durch wiederholtes Ziehen aus einer Stichprobe mit Zurücklegen. Abbildung aus [@Hesterberg2015], dort Figure 5. Die Publikation ist open-access und darf für nicht-kommerzielle Zwecke verwendet werden. [Link zur Lizenz](https://www.tandfonline.com/action/showCopyRight?scroll=top&doi=10.1080%2F00031305.2015.1089789)](figures/sampling_bootstrap.png)
Abbildung 8.3: Berechnen einer Stichprobenverteilung durch wiederholtes Ziehen aus einer Stichprobe mit Zurücklegen. Abbildung aus (Hesterberg 2015), dort Figure 5. Die Publikation ist open-access und darf für nicht-kommerzielle Zwecke verwendet werden. Link zur Lizenz
Die Konfidenzintervalle berechnet man aus der Stichprobenverteilung der Bootstrap-Stichproben, indem man z.B. das 2.5% und das 97.5% Quantil berechnet. Zwischen diesen beiden Quantilen sind 95% der Werte enthalten. Dieses Intervall nennt man das 95%-Konfidenzintervall.
8.2 Konfidenzintervall für den Mittelwert der Anreisezeit
Wir sehen uns das Ganze anhand des Beispiels der Studierenden aus Werdeschlau an. Zunächst wieder der Code für die Simulation der Grundgesamtheit.
set.seed(123)
student_id <- 1:12000
anreise <- c(runif(n = 12000 * 0.8, min = 5, max = 40),
runif(n = 12000 * 0.2, min = 60, max = 120))
geschlecht <- sample(c('m', 'w'), size = 12000, replace = TRUE)
wohnort <- sapply(anreise, function(x) {
if(x < 30) 'stadt'
else 'land'
})
verkehrsmittel <- sapply(anreise, function(x) {
if(x <= 10) 'zu_fuss'
else if(x > 10 & x <= 15) sample(c('zu_fuss', 'fahrrad'), size = 1)
else if(x > 15 & x <= 45) sample(c('bus', 'fahrrad', 'auto'), size = 1)
else sample(c('bus', 'auto'), size = 1)
})
zeit_bib <- 5 * 60 - 0.7 * anreise + rnorm(length(anreise), 0, 20)
grundgesamtheit <- tibble(student_id, geschlecht, wohnort, verkehrsmittel, anreise, zeit_bib)
grundgesamtheit## # A tibble: 12,000 × 6
## student_id geschlecht wohnort verkehrsmittel anreise zeit_bib
## <int> <chr> <chr> <chr> <dbl> <dbl>
## 1 1 w stadt bus 15.1 294.
## 2 2 w land fahrrad 32.6 254.
## 3 3 w stadt fahrrad 19.3 231.
## 4 4 m land auto 35.9 245.
## 5 5 m land bus 37.9 234.
## 6 6 w stadt zu_fuss 6.59 303.
## 7 7 w stadt bus 23.5 284.
## 8 8 m land auto 36.2 274.
## 9 9 m stadt fahrrad 24.3 299.
## 10 10 w stadt bus 21.0 282.
## # … with 11,990 more rowsNun befragen wir 200 Studierende.
set.seed(345)
befragung_size <- 200
befragung <- rep_sample_n(grundgesamtheit, size = befragung_size, replace = FALSE, reps = 1)
befragung## # A tibble: 200 × 7
## # Groups: replicate [1]
## replicate student_id geschlecht wohnort verkehrsmittel anreise zeit_bib
## <int> <int> <chr> <chr> <chr> <dbl> <dbl>
## 1 1 1623 m stadt zu_fuss 7.06 299.
## 2 1 9171 m stadt fahrrad 11.3 278.
## 3 1 10207 w land bus 107. 199.
## 4 1 3506 w stadt bus 25.0 326.
## 5 1 8892 w stadt bus 28.1 259.
## 6 1 5460 m stadt bus 23.6 299.
## 7 1 6120 w stadt bus 20.0 268.
## 8 1 865 w stadt fahrrad 26.6 290.
## 9 1 11586 m land bus 114. 207.
## 10 1 8153 w stadt zu_fuss 8.06 297.
## # … with 190 more rowsWir berechnen den wahren Mittelwert der Anreisezeit und den Mittelwert aus der Befragung.
mean_grundgesamtheit <- grundgesamtheit %>%
summarise(Mittelwert = mean(anreise))
mean_grundgesamtheit## # A tibble: 1 × 1
## Mittelwert
## <dbl>
## 1 36.0## # A tibble: 1 × 2
## replicate Mittelwert
## <int> <dbl>
## 1 1 34.1Wir ziehen jetzt unsere Bootstrap-Stichproben aus der einen Stichprobe, nämlich der befragung. Achten Sie darauf, wie ähnlich der Code zum Ziehen von echten Stichproben ist. Wir ändern nur replace = TRUE.
set.seed(345)
befragung_size <- 200
number_reps <- 10000
befragung_reps_bootstrap <- rep_sample_n(befragung, size = befragung_size, replace = TRUE, reps = number_reps)
befragung_reps_bootstrap## # A tibble: 2,000,000 × 7
## # Groups: replicate [10,000]
## replicate student_id geschlecht wohnort verkehrsmittel anreise zeit_bib
## <int> <int> <chr> <chr> <chr> <dbl> <dbl>
## 1 1 7038 m stadt bus 29.4 243.
## 2 1 493 m stadt bus 21.1 303.
## 3 1 3442 m land auto 30.3 311.
## 4 1 4920 w stadt bus 21.1 290.
## 5 1 3178 w stadt zu_fuss 8.07 325.
## 6 1 7694 w land auto 31.3 295.
## 7 1 9479 m land bus 39.5 302.
## 8 1 3367 m land auto 36.4 272.
## 9 1 5985 w stadt fahrrad 15.9 303.
## 10 1 843 m stadt fahrrad 26.4 300.
## # … with 1,999,990 more rowsStudierende kommen jetzt mehrfach vor, da wir ja mit Zurücklegen gezogen haben. Wir sehen uns das in den erste 50 Bootstrap-Stichproben an.
befragung_reps_bootstrap %>%
filter(replicate %in% (1:50)) %>%
group_by(replicate, student_id) %>%
tally() %>%
filter(n != 1) %>%
arrange(desc(n))## # A tibble: 2,657 × 3
## # Groups: replicate [50]
## replicate student_id n
## <int> <int> <int>
## 1 43 4787 8
## 2 20 5985 6
## 3 34 7749 6
## 4 38 5641 6
## 5 41 8456 6
## 6 3 7083 5
## 7 3 10943 5
## 8 5 8994 5
## 9 6 10118 5
## 10 8 11425 5
## # … with 2,647 more rowsJetzt berechnen wir die Mittelwerte aus den Bootstrap-Stichproben.
res_means_bootstrap <- befragung_reps_bootstrap %>%
group_by(replicate) %>%
summarise(Mittelwert = mean(anreise))
res_means_bootstrap## # A tibble: 10,000 × 2
## replicate Mittelwert
## <int> <dbl>
## 1 1 32.6
## 2 2 31.9
## 3 3 38.9
## 4 4 33.5
## 5 5 35.4
## 6 6 37.2
## 7 7 34.4
## 8 8 33.4
## 9 9 35.5
## 10 10 31.0
## # … with 9,990 more rowsDer Standardfehler des Bootstraps und das 95%-Konfidenzintervall basierend auf Quantilen berechnen sich wie folgt:
stat_bootstrap <- res_means_bootstrap %>%
summarize(mean = mean(Mittelwert), sd = sd(Mittelwert), ci_2.5 = quantile(Mittelwert, probs = 0.025), ci_97.5 = quantile(Mittelwert, probs = 0.975))Wir stellen die Stichprobenverteilung mit dem Standardfehler des Bootstraps und dem 95%-Konfidenzintervall dar. Das ist eine umfangreiche Grafik und wir gehen in der Übung Schritt für Schritt vor. Die Funktion scale_color_manual erlaubt es uns, die Legende anzupassen.
ggplot(res_means_bootstrap, aes(Mittelwert)) +
geom_histogram(bins = 50 , color="white") +
labs(y = 'Häufigkeit', x = 'Mittelwerte der Anreise (min)') +
geom_vline(aes(xintercept = mean_grundgesamtheit$Mittelwert, col = 'grundgesamtheit'), linetype = "dashed", size = 2) +
geom_vline(aes(xintercept = stat_bootstrap$mean, col = 'boot')) +
geom_vline(aes(xintercept = mean_befragung$Mittelwert, col = 'stichprobe'), linetype = 'dashed', size = 2) +
geom_vline(aes(xintercept = stat_bootstrap$mean + stat_bootstrap$sd, col = 'sd')) +
geom_vline(xintercept = stat_bootstrap$mean - stat_bootstrap$sd, col = 'orange') +
geom_vline(aes(xintercept = stat_bootstrap$ci_2.5, col = 'ci')) +
geom_vline(xintercept = stat_bootstrap$ci_97.5, col = 'brown') +
scale_color_manual(name = "Statistik", values = c(grundgesamtheit = 'black', sd = 'orange', boot = 'red', ci = 'brown', stichprobe = 'gray90'), breaks = c('stichprobe', 'boot', 'sd', 'ci', 'grundgesamtheit'), label = c('Mittelwert Stichprobe', 'Mittelwert Bootstrap', 'Standardfehler Bootstrap', '95% Konfidenzintervall Bootstrap', 'Mittelwert Population'))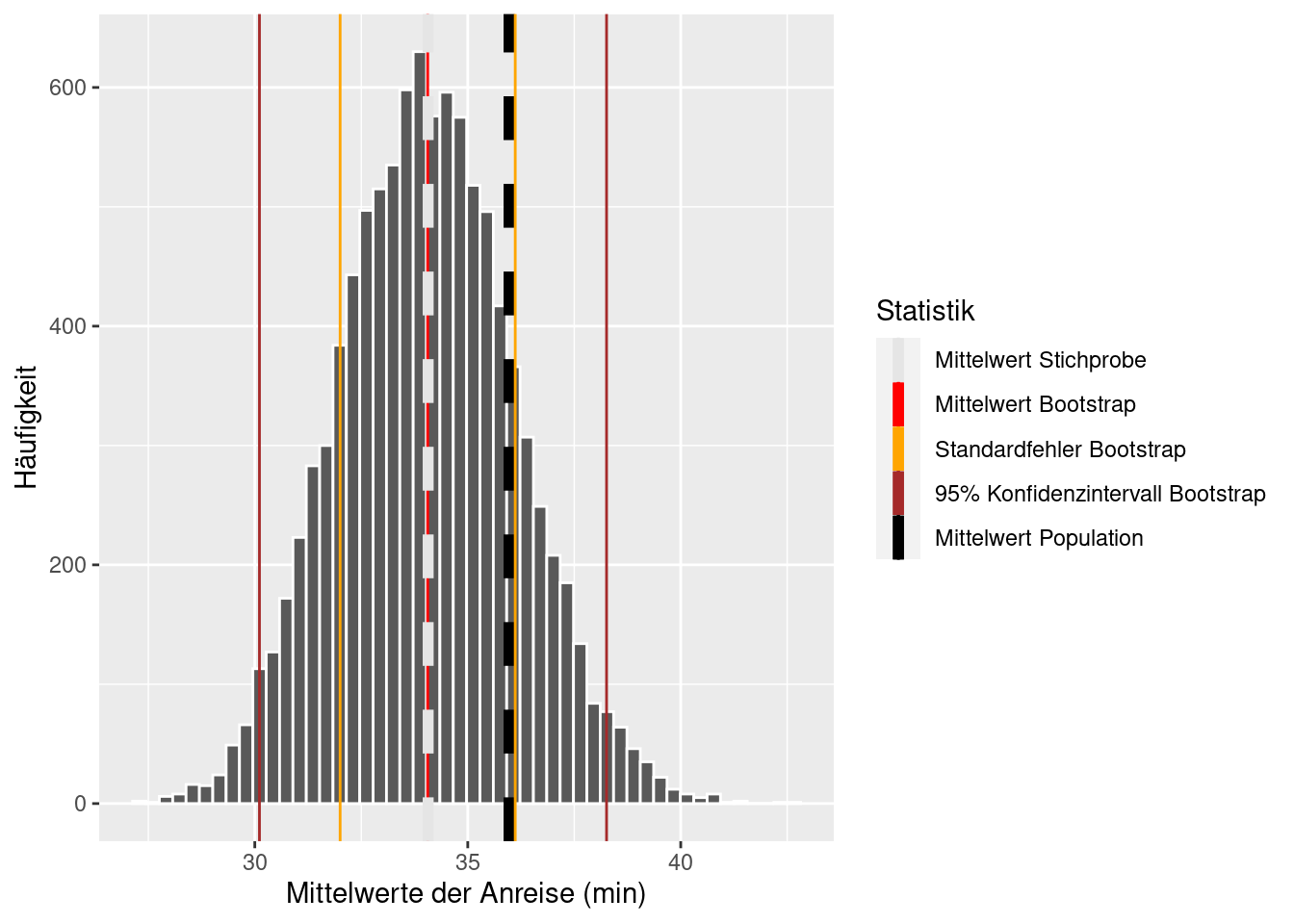
Der Standardfehler des Bootstraps stimmt gut mit dem Fehler \(s/\sqrt(n)\) für den Schätzer des Mittelwerts überein. Diese Formel nutzt die Normalverteilung des Schätzers aus. Da wir normalerweise die wahre Standardabweichung der Grundgesamtheit nicht kennen, wird in der Formel \(s/\sqrt(n)\) die Standardabweichung der Stichprobe als Schätzung verwendet.
## # A tibble: 1 × 2
## replicate sd_error
## <int> <dbl>
## 1 1 2.04Standardfehler des Bootstraps.
## # A tibble: 1 × 1
## sd_error
## <dbl>
## 1 2.06Und der wahre Standardfehler, wenn man die Standardabweichung der Grundgesamtheit kennt.
## # A tibble: 1 × 1
## sd_error
## <dbl>
## 1 2.09
8.3 Bootstrap-Konfidenzintervalle mit infer
Das Paket infer bietet eine sehr bequeme Möglichkeit, Konfidenzintervalle mit Bootstrap zu berechnen und zu visualisieren. Das Vorgehen aus dem vorherigen Abschnitt übertragen wir nun in den Workflow mit infer.
Berechnen der Bootstrap-Stichproben.
set.seed(345)
bootstrap_distribution <- befragung %>%
specify(response = anreise) %>%
generate(reps = 10000, type = 'bootstrap') %>%
calculate(stat = 'mean')Visualisieren der Stichprobenverteilung.
visualize(bootstrap_distribution)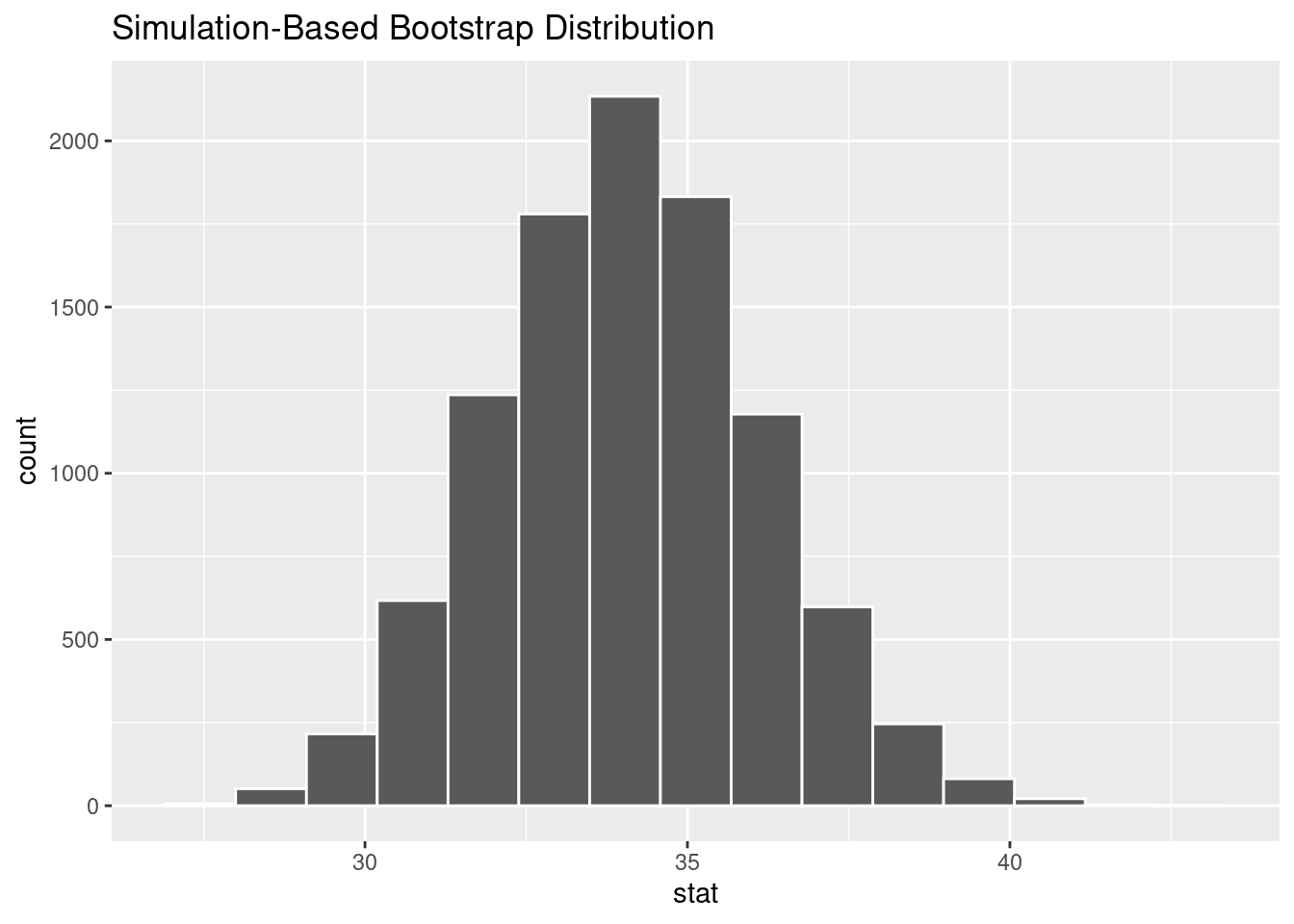
Berechnen Konfidenzintervalle
percentile_ci <- bootstrap_distribution %>%
get_confidence_interval(level = 0.95, type = "percentile")
percentile_ci## # A tibble: 1 × 2
## lower_ci upper_ci
## <dbl> <dbl>
## 1 30.1 38.3Visualisieren der Stichprobenverteilung mit den Konfidenzintervallen
visualize(bootstrap_distribution) +
shade_confidence_interval(endpoints = percentile_ci, color = "orange", fill = "khaki") +
geom_vline(xintercept = mean_grundgesamtheit$Mittelwert, linetype = 'dashed')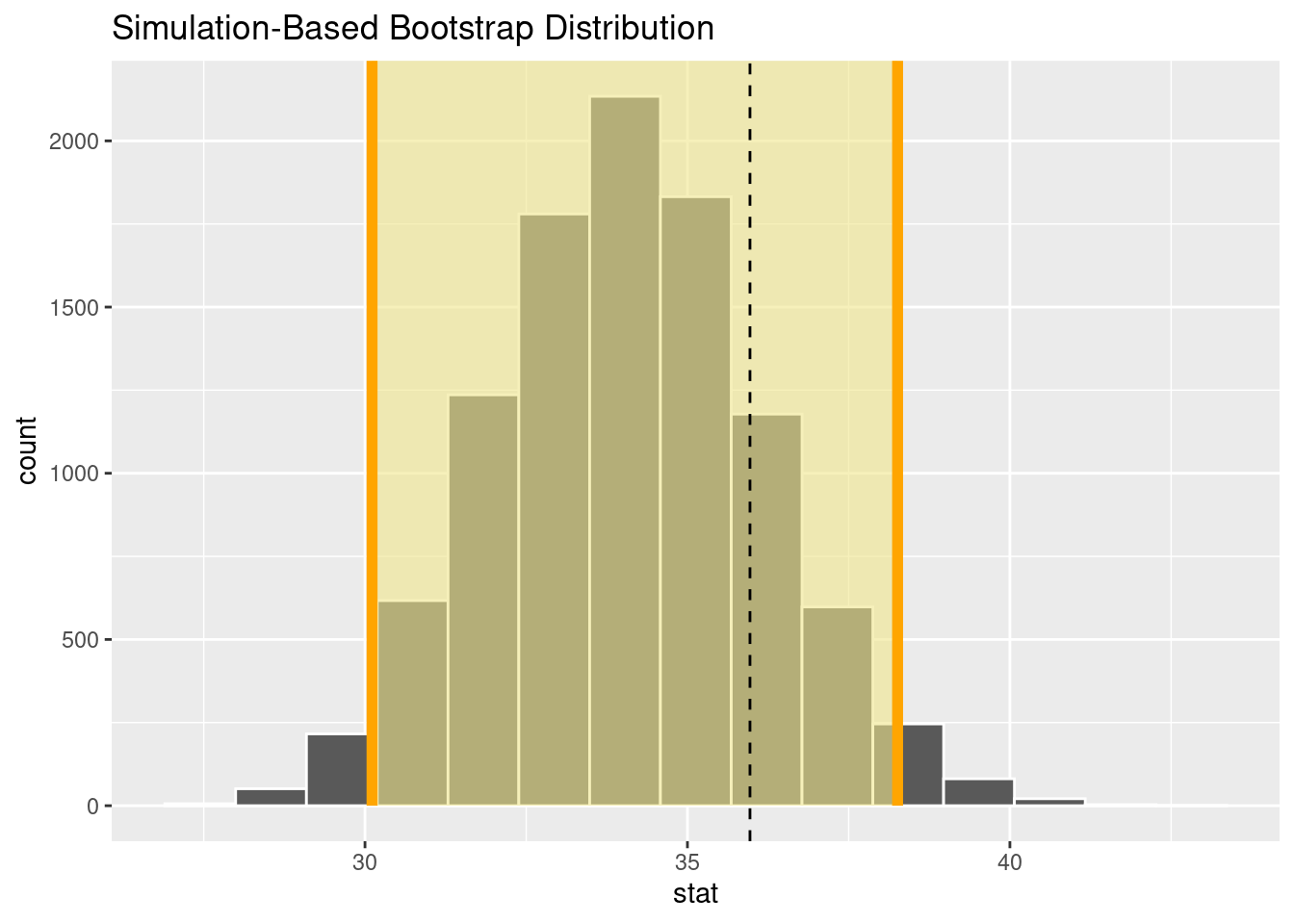
Die Konfidenzintervalle, die wir als Quantile aus der Bootstrap-Stichprobenverteilung berechnet haben, und die, die man mit der Formel \(\hat{\mu} \pm 1.96 \cdot s/\sqrt(n)\) berechnen kann, sind ähnlich. Das werden Sie in einer der Aufgaben (s.u.) nachrechnen. Das liegt daran, dass der Zentrale Grenzwertsatz garantiert, dass die Stichprobenverteilung des Schätzers des Mittelwerts eine Normalverteilung ist. Es gibt aber Schätzer, wie den des Medians, für den es keine theoretische Verteilung gibt. Daher gilt als Take-Home-Message, dass man Bootstrap zum Berechnen der Konfidenzintervalle gut einsetzen kann, egal ob es eine theoretische Verteilung des Schätzers gibt. Die Quantilmethode zur Berechnung der Bootstrap-Konfidenzintervalle liefert gute Ergebnisse. Wir werden im späteren Kapitel lernen, dass man Bootstrap auch für die Regressionsanalyse nutzen kann.
8.4 Bedeutung der Konfidenzintervalle
Ein Konfidenzintervall hängt von der Stichprobe ab, ist also vom Zufall betroffen. Man kann also sagen, dass die Grenzen des Konfidenzintervalls Zufallsvariablen sind. Das Konfidenzintervall wird nicht immer den wahren Parameter der Grundgesamtheit einschließen. Die Definition eines 95%-Konfidenzintervalls kann wie folgt formuliert werden:
Wenn wir sehr oft die Stichproben neu ziehen und jedes Mal ein 95%-Konfidenzintervall berechnen, dann erwarten wir, dass in 95% der Fälle diese Konfidenzintervalle den wahren Parameter der Grundgesamtheit enthalten.
Das Konfidenzintervall ist unsere Abschätzung der Lage des wahren Parameters der Grundgesamtheit. Die Interpretation wird oft so abgekürzt, dass man sagt, man sei zu 95% sicher, dass das 95%-Konfidenzintervall den wahren Parameter enthält. Das ist nicht richtig (s. Definition oben). Es ist besser zu sagen, dass in 95% der Fälle, das Konfidenzintervall den wahren Parameter der Grundgesamtheit enthält. Was mit 95% der Fälle gemeint ist, wissen Sie ja, wenn Sie sich an die genaue Definition erinnern 😄.
8.5 Lesestoff
Kapitel 8 in Ismay and Kim (2021)
8.6 Aufgaben
8.6.1 Konfidenzintervall aus dem Zentralen Grenzwertsatz
Der Zentrale Grenzwertsatz besagt, dass die Stichprobenverteilung des Schätzers des Mittelwerts sich asymptotisch (also bei vielen Stichproben) der Normalverteilung nähert. Daher kann man für die Konfidenzintervalle auch die folgende Formel nutzen: \(\hat{\mu} \pm 1.96 \cdot SE\), wobei \(\hat{\mu}\) der geschätzte Mittelwert ist. Das Hütchen steht für geschätzt.
- Berechnen Sie die Konfidenzintervalle mit dieser Formel für die Stichprobenverteilung aus dem Bootstrap für den Mittelwert der Anreisezeit. Dazu passen Sie in der Funktion
get_confidence_intervalden Typ des Konfidenzintervalls antype = "se"und geben Sie den Mittelwert der Befragung an:get_confidence_interval(type = "se", point_estimate = mean_befragung$Mittelwert). - Stellen Sie die Stichprobenverteilung mit diesem Konfidenzintervall dar und vergleichen Sie mit dem Konfidenzintervall, das wir mit der Quantil-Methode berechnet haben.
8.7 Ihre Arbeit einreichen
- Speichern Sie Ihr Notebook ab.
- Laden Sie Ihre .Rmd Datei in ILIAS hoch. Beachten Sie die Frist!
- Sie erhalten die Musterlösung nach dem Hochladen.
8.8 Weiterführende Literatur
Kapitel 17.3 in Sauer (2019)