Kapitel 10 Schätzen von Effekten: Raus aus der \(p < 0.05\)-Falle
- Unterschied zwischen einem Hypothesentest und der Schätzung von Effekten erklären
Bei Hypothesentests wird häufig ein willkürlich festgelegter Schwellenwert, das Signifikanzniveau, häufig 5%, verwendet. Liegt der \(p\)-Wert darunter, wird die Nullhypothese verworfen. Liegt er darüber, wird sie beibehalten.
Dieses starre Konzept der statistischen Signifikanz, bei dem ein willkürlich gesetzter Grenzwert \(\alpha\) darüber entscheidet, ob ein Ergebnis weiter beachtet wird oder nicht, wird seit Jahrzehnten kritisiert (Wasserstein, Schirm, and Lazar 2019). Es ist schließlich auch wirklich schwer zu verstehen, warum \(p = 0.049\) qualitativ etwas anderes aussagen soll als \(p = 0.051\). Und was machen wir mit \(p = 0.05\)? Die beste Lösung ist, so wie von der ASA (American Statistical Association) vorgeschlagen, den Begriff “signifikant” nicht mehr zu verwenden. Stattdessen berichten Sie den berechneten \(p\)-Wert und interpretieren ihn im wissenschaftlichen Kontext (Wasserstein, Schirm, and Lazar 2019).
Ich würde nicht so weit gehen, statistische Tests abschaffen zu wollen. Sie sind manchmal nützlich, aber auch nicht häufiger als manchmal. Allerdings kann ich auch aus eigener Praxis sagen, dass häufig statistische Signifikanz mit wissenschaftlicher Relevanz verwechselt wird. Daher werden wir uns in diesem Kapitel damit beschäftigen, wie man die relevanten Aspekte, nämlich die Größe des Effekts, aus den beobachteten Daten schätzen kann.
10.1 Größe des Effekts
Daten sind immer mit Unsicherheiten behaftet. Modelle und Tests haben Annahmen, z.B. dass die gewählte Statistik oder das Modell der Nullhypothese für die Forschungsfrage geeignet sind. Diese Unsicherheit gilt es richtig zu erfassen und zu berichten. Daher ist es wichtig, für jede Schätzung entweder ein Konfidenzintervall anzugeben oder den Standardfehler (Wasserstein, Schirm, and Lazar 2019).
Wir werden zum Schätzen von Effekten für einfache statistische Analysen das Paket dabestr (https://github.com/ACCLAB/dabestr) benutzen. Es bietet die Möglichkeit, Effekte zu schätzen, Bootstrap-Konfidenzintervalle zu berechnen und das Ganze in sehr ansprechenden Grafiken zu visualisieren. Zu dem Paket gibt es eine Publikation, Ho et al. (2019), die ich sehr empfehlen kann. Konfidenzintervalle und die (einige einfache) Effekte können wir auch mit infer berechnen. Der größte Vorteil von dabestr sind die tollen Grafiken.
Effekte ist ein sehr allgemeiner Begriff. In unterschiedlichen Kontexten und Fächern werden unterschiedliche Formeln dafür verwendet. dabestrbietet eine Reihe davon an (s.u.). Im Zweifelsfall lesen Sie nach, wie “Effekte” für Ihre Fragestellung definiert werden.
10.2 Schätzen des Effekts mit dem Bootstrap – dabestr
Wir laden die nötigen Bibliotheken.
und holen uns wieder unsere Lieblingsgrundgesamtheit und Befragung 😄.
set.seed(123)
student_id <- 1:12000
anreise <- c(runif(n = 12000 * 0.8, min = 5, max = 40),
runif(n = 12000 * 0.2, min = 60, max = 120))
geschlecht <- sample(c('m', 'w'), size = 12000, replace = TRUE)
wohnort <- sapply(anreise, function(x) {
if(x < 30) 'stadt'
else 'land'
})
verkehrsmittel <- sapply(anreise, function(x) {
if(x <= 10) 'zu_fuss'
else if(x > 10 & x <= 15) sample(c('zu_fuss', 'fahrrad'), size = 1)
else if(x > 15 & x <= 45) sample(c('bus', 'fahrrad', 'auto'), size = 1)
else sample(c('bus', 'auto'), size = 1)
})
zeit_bib <- 5 * 60 - 0.7 * anreise + rnorm(length(anreise), 0, 20)
grundgesamtheit <- tibble(student_id, geschlecht, wohnort, verkehrsmittel, anreise, zeit_bib)
datatable(grundgesamtheit, options = list(scrollX = T)) %>%
formatRound(c('zeit_bib', 'anreise'), 1)
set.seed(345)
befragung_size <- 200
befragung <- rep_sample_n(grundgesamtheit, size = befragung_size, replace = FALSE, reps = 1)
datatable(befragung, options = list(scrollX = T)) %>%
formatRound(c('zeit_bib', 'anreise'), 1)Wir würden gerne den Unterschied der Arbeitszeit in der Bibliothek zwischen Männern und Frauen kennen. D.h. wir möchten diesen Unterschied schätzen und auch die Unsicherheit der Schätzung quantifizieren. Ich hoffe, der Wortlaut kommt Ihnen bekannt vor 🤓.
Die wichtigste Funktion in dabestr heißt dabest(). Sie erstellt einen tidy tibble im richtigen Format für die Schätzung und das Bootstrap. Aktuell können Sie mit dabestr folgende Effekte schätzen:
- Differenz zwischen Mittelwerten von Gruppen mit
mean_diff(). - Differenz zwischen Medianen von Gruppen mit
median_diff(). - Cohen’s d mit
cohens_d(). Cohen’s d ist die Differenz zwischen Mittelwerten geteilt durch die Standardabweichung der Daten. - Hedges’ g mit
hedges_g(). Ähnlich wie Cohen’s d, aber etwas besser für kleine Datensätze. - Cliff’s delta mit
cliffs_delta(). Entwickelt für ordinalskalierte Daten, überprüft, wie oft Datenpunkte in einer Gruppe größer sind als Datenpunkte in einer Vergleichsgruppe.
Wir stellen unsere Daten mithilfe von dabest() zusammen. Der Parameter idx gibt an, wie die Differenz berechnet wird, nämlich Männer - Frauen.
diff_zeit_bib <- befragung %>%
dabest(x = geschlecht, y = zeit_bib,
idx = c('w', 'm'),
paired = FALSE)Wir sehen uns mit dabest() erstellten Datensatz an.
diff_zeit_bib## dabestr (Data Analysis with Bootstrap Estimation in R) v0.3.0
## =============================================================
##
## Good afternoon!
## The current time is 16:38 on Samstag Oktober 15, 2022.
##
## Dataset : .
## The first five rows are:
## # A tibble: 5 × 7
## # Groups: replicate [1]
## replicate student_id geschlecht wohnort verkehrsmittel anreise zeit_bib
## <int> <int> <fct> <chr> <chr> <dbl> <dbl>
## 1 1 1623 m stadt zu_fuss 7.06 299.
## 2 1 9171 m stadt fahrrad 11.3 278.
## 3 1 10207 w land bus 107. 199.
## 4 1 3506 w stadt bus 25.0 326.
## 5 1 8892 w stadt bus 28.1 259.
##
## X Variable : geschlecht
## Y Variable : zeit_bib
##
## Effect sizes(s) will be computed for:
## 1. m minus wWir berechnen die Unterschiede in Mittelwerten von zeit_bib zwischen den Geschlechtern und bootstrappen in einem Schritt.
## dabestr (Data Analysis with Bootstrap Estimation in R) v0.3.0
## =============================================================
##
## Good afternoon!
## The current time is 16:38 on Samstag Oktober 15, 2022.
##
## Dataset : .
## X Variable : geschlecht
## Y Variable : zeit_bib
##
## Unpaired mean difference of m (n = 105) minus w (n = 95)
## -4.41 [95CI -12.9; 4.2]
##
##
## 10000 bootstrap resamples.
## All confidence intervals are bias-corrected and accelerated.Sie bekommen die Rückmeldung, dass ungepaarte Differenzen zwischen den Gruppen ausgerechnet wurden. Ungepaart bedeutet, dass die Frauen und Männer statistisch nicht verbunden sind. Etwas anderes wäre es, wenn man dieselben Studierenden wiederholt befragen würde (und dazwischen z.B. etwas unternehmen würde, um deren Meinung zu beeinflussen). Weiterhin zeigt Ihnen dabest auch gleich die Bootstrap-Konfidenzintervalle.
Die Schätzung des Unterschieds stellen wir in einem Gardner-Altman-Plot dar (Gardner and Altman 1986). Wir beschriften die Grafik gleich sinnvoll und schalten die Legende ab, da sie in diesem Fall redundant ist.
plot(mean_diff_zeit_bib, color.column = geschlecht, rawplot.ylabel = 'Zeit in der Bibliothek (min)', effsize.ylabel = 'Ungepaarte mittlere Differenz', show.legend = F)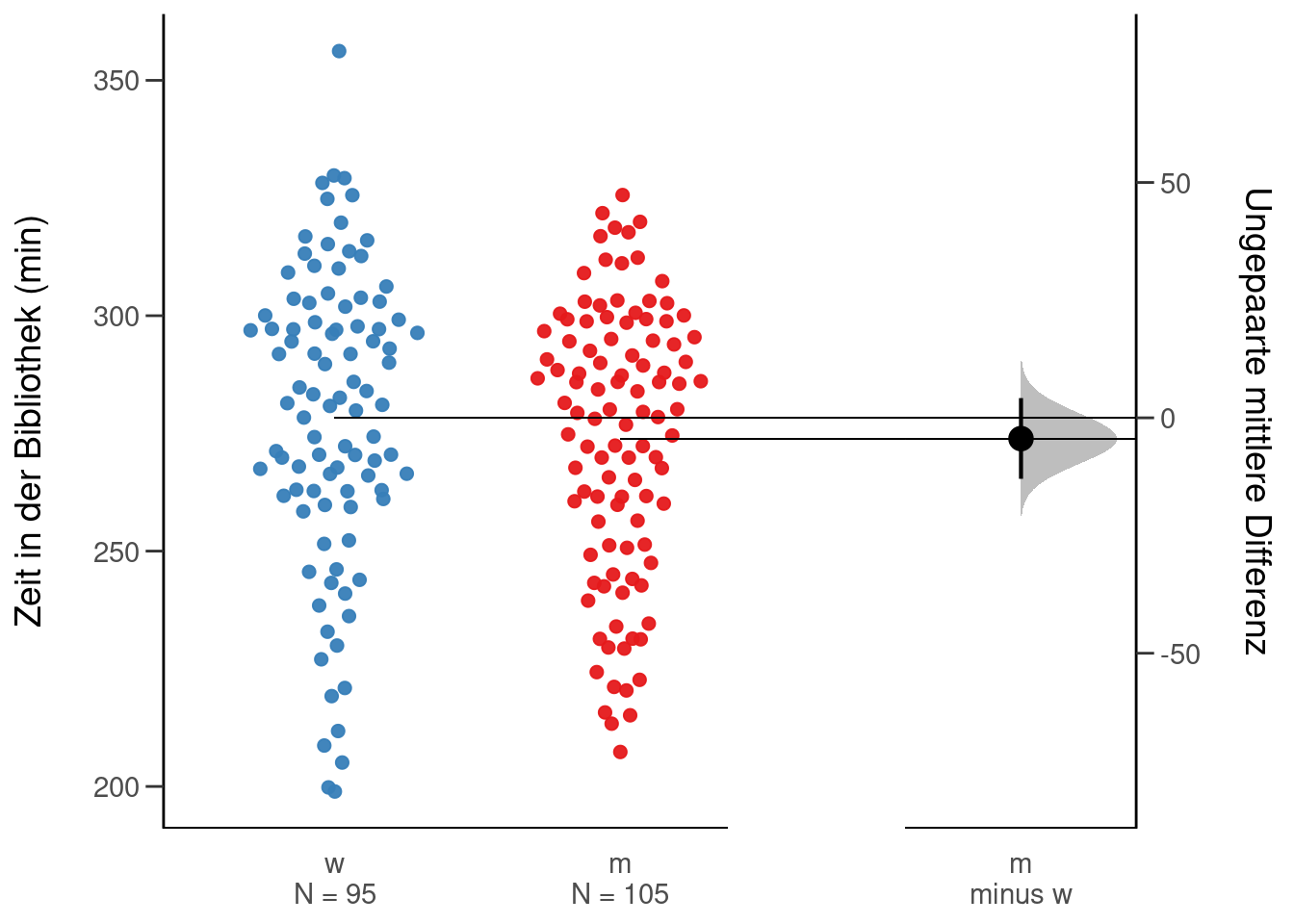
In der Abbildung können Sie mehrere Dinge sehen:
- alle gemessenen Punkte (Zeiten in der Bibliothek). D.h. Sie können die Streuung der Daten erkennen. Das ist sehr informativ.
- die Schätzung der mittleren Differenz (dicker schwarzer Punkt) und als graue Fläche die Stichprobenverteilung aus dem Bootstrap.
- das 95%-Konfidenzintervall für die Schätzung (dicker schwarzer vertikaler Strich)
Wir können nun erkennen, dass die Schätzung recht genau ist, da das Konfidenzintervall schmal ist. Frauen scheinen mehr Zeit in der Bibliothek zu verbringen, da die geschätzte Differenz negativ ist. Das können wir genau abfragen, mit mean_diff_zeit_bib$result$difference. Das sind -4.4 Minuten. Dieser Unterschied ist für alle praktischen Belange irrelevant. Das Konfidenzintervall umfasst auch die Null, sodass kein Unterschied auch eine plausible Schätzung ist. Somit würden wir schließen, dass es nicht genug Evidenz für einen relevanten Unterschied in der Arbeitszeit in der Bibliothek zwischen Männern und Frauen gibt.
10.3 Welche Fragen soll ich mir bei der Analyse stellen?
Bei der statistischen Analyse Ihrer Daten sollten Sie sich vom “statistischen Denken” leiten lassen. Wasserstein, Schirm, and Lazar (2019) beschreibt es als
Accept uncertainty. Be thoughtful, open, and modest.
Denken Sie immer daran, dass Unsicherheit jedem Forschungsunterfangen innewohnt. Wenn Sie Ihre Daten interpretieren, stellen Sie sich folgende Fragen (Anderson 2019):
- Welche praktische Bedeutung hat meine Schätzung des Effekts? Ist er überhaupt relevant?
- Wie präzise ist die Schätzung?
- Passt das Modell zu meiner Forschungsfrage? Ist es korrekt formuliert?
10.4 Was dabest nicht kann, besorgt infer
Aktuell kann dabestr nicht mit Anteilen (proportions) arbeiten. Daher werden wir bei solchen Aufgaben auf unser bewährtes Framework in infer zurückgreifen.
10.5 Lesestoff
Ho et al. (2019)
10.6 Aufgaben
10.6.1 Bodenverdichtung, revisited
Wir kommen zurück zu Daten aus Aufgabe B.3.3. Wie stark hat sich die Lagerungsdichte auf den befahrenen Feldern verändert? Schätzen Sie den Effekt und geben Sie 95%-Konfidenzintervalle an. Vergleichen Sie die Aussagen, die Sie mit dieser Lösung treffen können, mit der Aussage aus dem Hypothesentest.
10.6.2 Anteil von beschäftigten Frauen im privaten und öffentlichen Sektor, revisited
Wir sehen uns erneut die Daten der Weltbank aus der Aufgabe B.3.4 an. Diesmal interessiert und die Schätzung des Anteils und ihr 95%-Bootstrap-Konfidenzintervall. Vergleichen Sie die Aussagen, die Sie mit dieser Lösung treffen können, mit der Aussage aus dem Hypothesentest.
10.7 Ihre Arbeit einreichen
- Speichern Sie Ihr Notebook ab.
- Laden Sie Ihre .Rmd Datei in ILIAS hoch. Beachten Sie die Frist!
- Sie erhalten die Musterlösung nach dem Hochladen.
10.8 Weitere Infos
- Vignette von
dabestr: https://cran.r-project.org/web/packages/dabestr/vignettes/using-dabestr.html