Kapitel 12 Inferenz in linearer Regression
- Konfidenzintervalle für Modellparameter berechnen
- Zusammenfassung eines linearen Modells in R interpretieren
- Bestimmtheitsmaß \(R^2\) erklären
- Konfidenzintervalle für nicht normalverteilte Residuen berechnen
Im letzten Kapitel haben wir die einfache Normalregression kennengelernt. Bevor wir die geschätzten Parameter und deren Konfidenzintervalle interpretieren, müssen wir die Annahmen der Normalregression überprüfen (hauptsächlich grafisch). Diese Annahmen sind:
- Der Zusammenhang zwischen der abhängigen und den erklärenden Variablen ist linear.
- Residuen sind unabhängig.
- Residuen haben einen Mittelwert von Null und sind homoskedastisch (gleiche Varianz).
- Residuen sind normalverteilt
In diesem Kapitel beschäftigen wir uns mit folgenden Fragen:
- Wie schätzt man die Parameter?
- Wie gut sind diese Schätzungen?
- Wie gut ist das Modell?
- Was macht man, wenn die Residuen nicht normalverteilt sind?
12.1 Zurück zum Beispiel: Anreisezeit und Arbeitszeit in der Bibliothek
12.1.1 Parameter und Konfidenzintervalle schätzen
Woher kommen die Schätzungen der Modellparameter und deren Konfidenzintervalle in unserem Modell? Dieses Kapitel basiert auf den theoretischen Herleitungen aus Fahrmeir, Kneib, and Lang (2009).
lin_mod <- lm(zeit_bib ~ anreise, data = befragung)
get_regression_table(lin_mod) %>% kable()| term | estimate | std_error | statistic | p_value | lower_ci | upper_ci |
|---|---|---|---|---|---|---|
| intercept | 302.094 | 2.282 | 132.387 | 0 | 297.594 | 306.594 |
| anreise | -0.766 | 0.051 | -14.990 | 0 | -0.867 | -0.665 |
Eine häufig verwendete Methode, die Modellparameter zu schätzen, heißt Methode der kleinsten Quadrate (KQ). Sie beruht auf der Idee, dass diejenigen Modellparameter, \(y\)-Achsenabschnitt und die Steigung, die besten sind, bei denen die Summe der quadrierten Residuen die kleinste ist. Formal schreibt man:
Gegeben sei das lineare Regressionsmodell
\[y_i=\beta_0 + \beta_1 x_i + \varepsilon_i\]
Um die unbekannten Parameter \(\beta_0\) und \(\beta_1\) zu bestimmen, minimiere die Summe der quadrierten Abweichungen
\[\mathrm{KQ}(\beta_0, \beta_1)=\sum_{i=1}^n (y_i - (\beta_0 + \beta_1 x_i))^2=\sum_{i=n}^n \varepsilon_i^2 \rightarrow \operatorname*{min}_{\beta_0,\, \beta_1}\]
Dann heißt \[ \boldsymbol{\hat{\beta}}=(\hat{\beta}_0, \hat{\beta}_1)\]
der Kleinste-Quadrate-Schätzer für den Parametervektor \(\boldsymbol{\beta} = (\beta_0, \beta_1)\).
Es geht also darum, die Residuen zu minimieren, d.h. die Abstände zwischen den beobachteten und den im Modell vorhergesagten Werten so klein wie möglich zu machen.
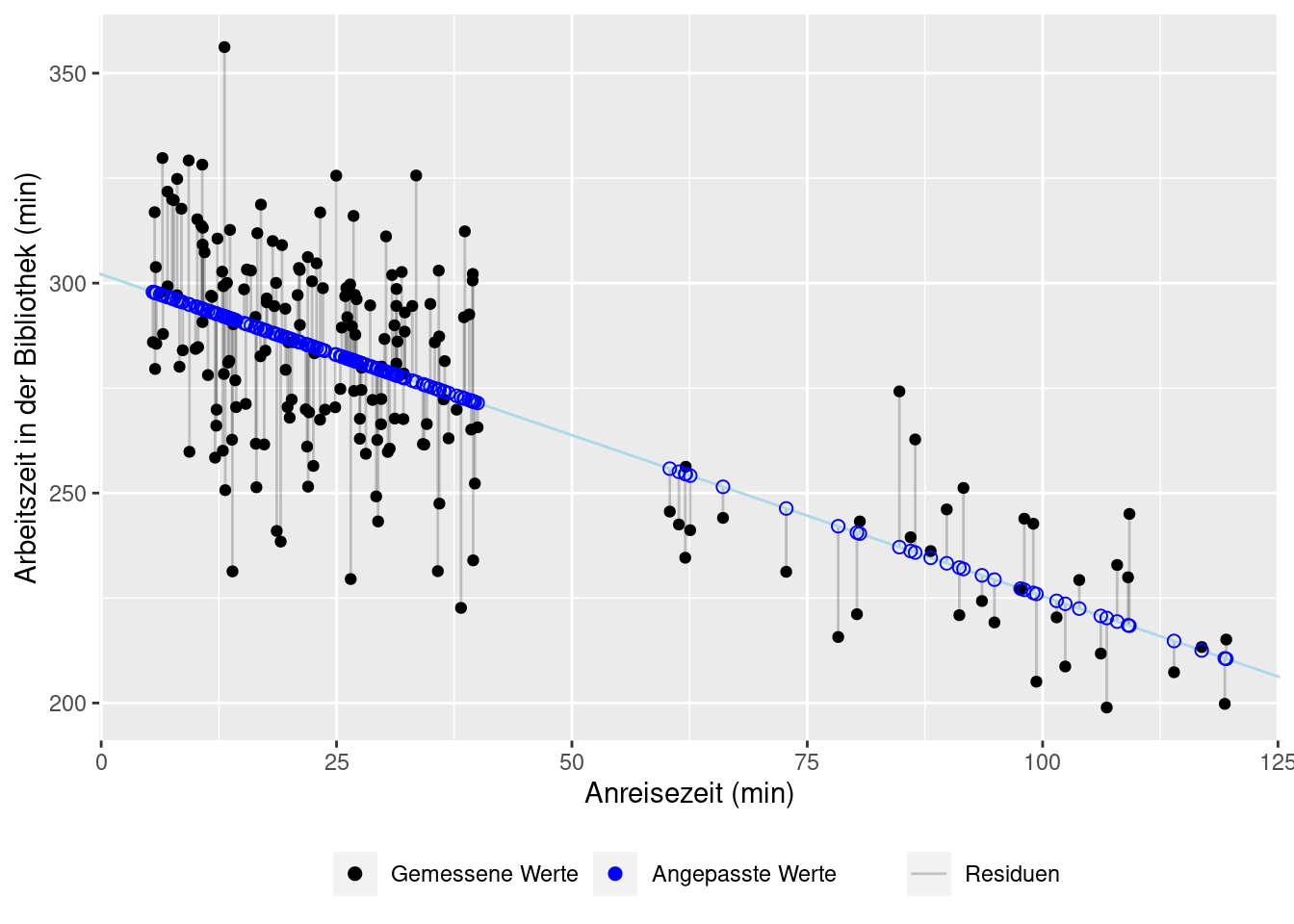
Man quadriert die Residuen, damit sowohl die positiven als auch die negativen gleich wichtig sind und sich in der Summe nicht gegenseitig aufheben.
Die Methode der kleinsten Quadrate ergibt folgende Formeln für die Schätzung der Modellparameter einer Einfachregression:
\[ \begin{align*} \hat{\sigma}^2 &= \frac{1}{n-2} \sum_{i=n}^n \varepsilon_i^2 \\ \hat{\beta}_0 &= \bar{y} - \hat{\beta}_1 \bar{x}\\ \hat{\beta}_1 &= \frac{\sum^n_{i=1} (x_i - \bar{x})(y_i - \bar{y})}{\sum^n_{i=1} (x_i - \bar{x})^2} \end{align*} \] Die Residuen \(\hat{\varepsilon}_i\) berechnen sich als die Differenz zwischen den beobachteten und den im Modell berechneten Werten:
\[\hat{\varepsilon}_i = y_i - \hat{y}_i\] und die angepassten Werte als Punkte auf der Regressionsgeraden:
\[\hat{y}_i = \hat{\beta}_0 + \hat{\beta}_1 x_i\]
Die geschätzten Modellparameter sind Zufallsvariablen. Denn wenn die Daten etwas anders ausfallen (Zufallsstichproben!), bekommen wir andere Schätzungen für den \(y\)-Achsenabschnitt und die Steigung. Unter der Annahme, dass die Residuen normalverteilt sind, d.h.:
\[\varepsilon_i \sim \mathcal{N}(0,\sigma^2)\] gilt für diese Zufallsvariablen, dass sie selbst normalverteilt sind:
\[\hat{\beta}_0 \sim \mathcal{N}(\beta_0, \sigma^2_{\hat{\beta}_0}), \qquad \hat{\beta}_1 \sim \mathcal{N}(\beta_1, \sigma^2_{\hat{\beta}_1})\]
Ihre Varianzen \(\sigma^2_{\hat{\beta}_0}\) und \(\sigma^2_{\hat{\beta}_1}\) müssen geschätzt werden:
\[\hat{\sigma}_{\hat{\beta}_0} = \hat{\sigma} \frac{\sqrt{\textstyle \sum_{i=1}^n x_i^2}}{\sqrt{n \textstyle \sum_{i=1}^n (x_i-\bar{x})^2}}, \quad \hat{\sigma}_{\hat{\beta}_1} = \frac{\hat{\sigma}}{\sqrt{\textstyle \sum_{i=1}^n (x_i-\bar{x})^2}}\]
Wenn die Residuen normalverteilt sind, kann mann zeigen, dass die sogen. standardisierten Schätzer der \(t\)-Verteilung folgen:
\[\frac{\hat{\beta}_0 - \beta_0}{\hat{\sigma}_{\hat{\beta}_0}} \sim t_{n-2}, \quad \frac{\hat{\beta}_1 - \beta_1}{\hat{\sigma}_{\hat{\beta}_1}} \sim t_{n-2}\] \(n-2\) steht hier für die Anzahl der Freiheitsgrade in der \(t\)-Verteilung. \(n\) ist die Anzahl der Datenpunkte im Modell.
Somit wissen wir nun endlich, wie die Schätzungen für den \(y\)-Achsenabschnitt und die Steigung verteilt sind. Mit diesem Wissen können wir Konfidenzintervalle für diese Modellparameter berechnen:
\[\hat{\beta}_0 \pm \hat{\sigma}_{\hat{\beta}_0} t_{1-\alpha/2, n-2}, \qquad \hat{\beta}_1 \pm \hat{\sigma}_{\hat{\beta}_1} t_{1-\alpha/2, n-2}\]
Für \(\alpha\) setzt man passendes Konfidenzlevel ein, z.B. 5%, um das 95%-Konfidenzintervall zu erhalten.
12.1.2 Wie gut ist das Modell?
Welcher Anteil der Streuung der Daten lässt sich durch die Regression erklären?
Die Streuung im Modell besteht aus:
\[ \begin{align*} \mathit{SQT} &= \mathit{SQE} + \mathit{SQR}\\ \sum^{n}_{i = 1} (y_i-\bar{y})^2 &= \sum^{n}_{i=1} (\hat{y}_i - \bar{y})^2 + \sum^{n}_{i=1} (y_i - \hat{y}_i)^2\\ \end{align*} \]
mit \(y_i\): Messwerte, \(\bar{y}\): Mittelwert, \(\hat{y}_i\): angepasste Werte
- \(\mathit{SQT}\) Sum of squares total: Gesamtstreuung der Daten
- \(\mathit{SQE}\) Sum of squares explained: Streuung erklärt vom Modell
- \(\mathit{SQR}\) Sum of sqaures residual: Residualstreuung (vom Modell nicht erklärt)
Die \(\mathit{SQE}\) beschreibt die Variation der angepassten Werte um den Mittelwert der beobachteten Daten und \(\mathit{SQR}\) entspricht dem nicht erklärten Teil der Streuung. Das heißt, je kleiner die Residualstreuung, desto besser das Modell, weil es dann einen größeren Anteil der Streuung der Daten erklären kann. Das Verhältnis der Gesamtstreuung zur Residualstreuung nennt man das Bestimmtheitsmaß (oder auch Determinationskoeffizient). Dieser wird meistens mit \(R^2\) bezeichnet und ist definiert als:
\[R^2 = \frac{\mathit{SQE}}{\mathit{SQT}} = 1- \frac{\sum^{n}_{i=1} (y_i - \hat{y}_i)^2}{\sum^{n}_{i = 1} (y_i - \bar{y}_i)^2}\]
\(R^2\) liegt (normalerweise) zwischen 0 (schlechtes Modell) und 1 (perfekter Fit). \(R^2 < 0\) zeigt eine falsche Modellwahl (z.B. kein Achsenabschnitt, wenn dieser aber nötig ist).
Das \(R^2\) hat die unangenehme Eigenschaft, bei einer multiplen Regression immer zu steigen, wenn man zusätzliche Prädiktoren hinzunimmt. Diese Prädiktoren können auch ohne jeden Zusammenhang zur abhängigen Variablen stehen. Um dieses Problem zu korrigieren, hat man das adjustierte Bestimmtheitsmaß \(R^2_\text{ajd}\) eingeführt. Es “bestraft” für zusätzliche Prädiktoren \[R^2_\text{ajd} = 1 - (1 - R^2) \frac{n-1}{n - p - 1}\]
mit \(n\): Anzahl der Datenpunkte, \(p\): Anzahl der Prädiktoren (ohne \(y\)-Achsenabschnitt). \(R^2_\text{ajd}\) ist aussagekräftiger als \(R^2\) bei multipler Regression.
Zurück zu unserem Beispiel. Wie viel Streuung erklärt nun unser Modell? Wir sehen uns die tidy Zusammenfassung an.
get_regression_summaries(lin_mod) %>% kable()| r_squared | adj_r_squared | mse | rmse | sigma | statistic | p_value | df | nobs |
|---|---|---|---|---|---|---|---|---|
| 0.532 | 0.529 | 430.4021 | 20.74614 | 20.851 | 224.697 | 0 | 1 | 200 |
-
r_squared: Bestimmtheitsmaß \(R^2\) -
adj_r_squared: adjustiertes Bestimmtheitsmaß \(R^2_\text{ajd}\) -
mse: mittlerer quadratischer Fehler, berechnet alsmean(residuals(lin_mod)^2) -
rmse: Wurzel ausmse -
simga: Standardabweichung (i.e. Standardfehler) des Fehlerterms \(\varepsilon\) -
statistic: Wert der \(F\)-Statistik für den Hypothesentest mit H\(_0\): alle Modellparameter sind Null -
p-value: \(p\)-Wert zum Hypothesentest -
df: Freiheitsgrade, hier Anzahl der Prädiktoren -
nobst: Anzahl der Datenpunkte
Somit erklärt unser Modell 53% der Varianz der Daten.
12.2 Bootstrap mit infer: Konfidenzintervall für Steigung
Die \(t\)-Verteilung der Schätzungen gilt asymptotisch, d.h. bei großen Datensätzen, auch für nicht-normalverteilte Residuen (unter bestimmten Bedingungen, s. Fahrmeir, Kneib, and Lang (2009)). Allerdings erfordern nicht-normalverteilte Residuen, große Stichproben oder aber alternative Methoden zum Berechnen der Konfidenzintervalle. Auch heteroskedastische Residuen führen zu falschen Konfidenzintervallen und Hypothesentests. Bootstrap ist robust gegen die Verletzung beider Annahmen (Normalverteilung und Homoskedastizität der Residuen). Allerdings müssen die Daten auch hierfür unabhängig sein (keine wiederholten Messungen, keine Zeitreihen!), damit Bootstrap korrekt arbeitet.
Bei einer Einfachregression, d.h., wenn es nur einen Prädiktor gibt, ist die Steigung häufig der interessante Parameter. Wenn wir uns also nicht für den \(y\)-Achsenabschnitt interessieren, dann können wir das altbekannte Framework von infer für das Bootstrap-Konfidenzintervall für die Steigung verwenden. Für unser Beispiel ginge es so:
Schritt 1: Bootstrap-Stichproben generieren und Statistik “Steigung” berechnen
bootstrap_distn_slope <- befragung %>%
specify(formula = zeit_bib ~ anreise) %>%
generate(reps = 10000, type = "bootstrap") %>%
calculate(stat = "slope")Schritt 2: Konfidenzintervall berechnen
percentile_ci <- bootstrap_distn_slope %>%
get_confidence_interval(type = "percentile", level = 0.95)
percentile_ci## # A tibble: 1 × 2
## lower_ci upper_ci
## <dbl> <dbl>
## 1 -0.848 -0.687Schritt 3: Ergebnisse darstellen
visualize(bootstrap_distn_slope) +
shade_confidence_interval(endpoints = percentile_ci) 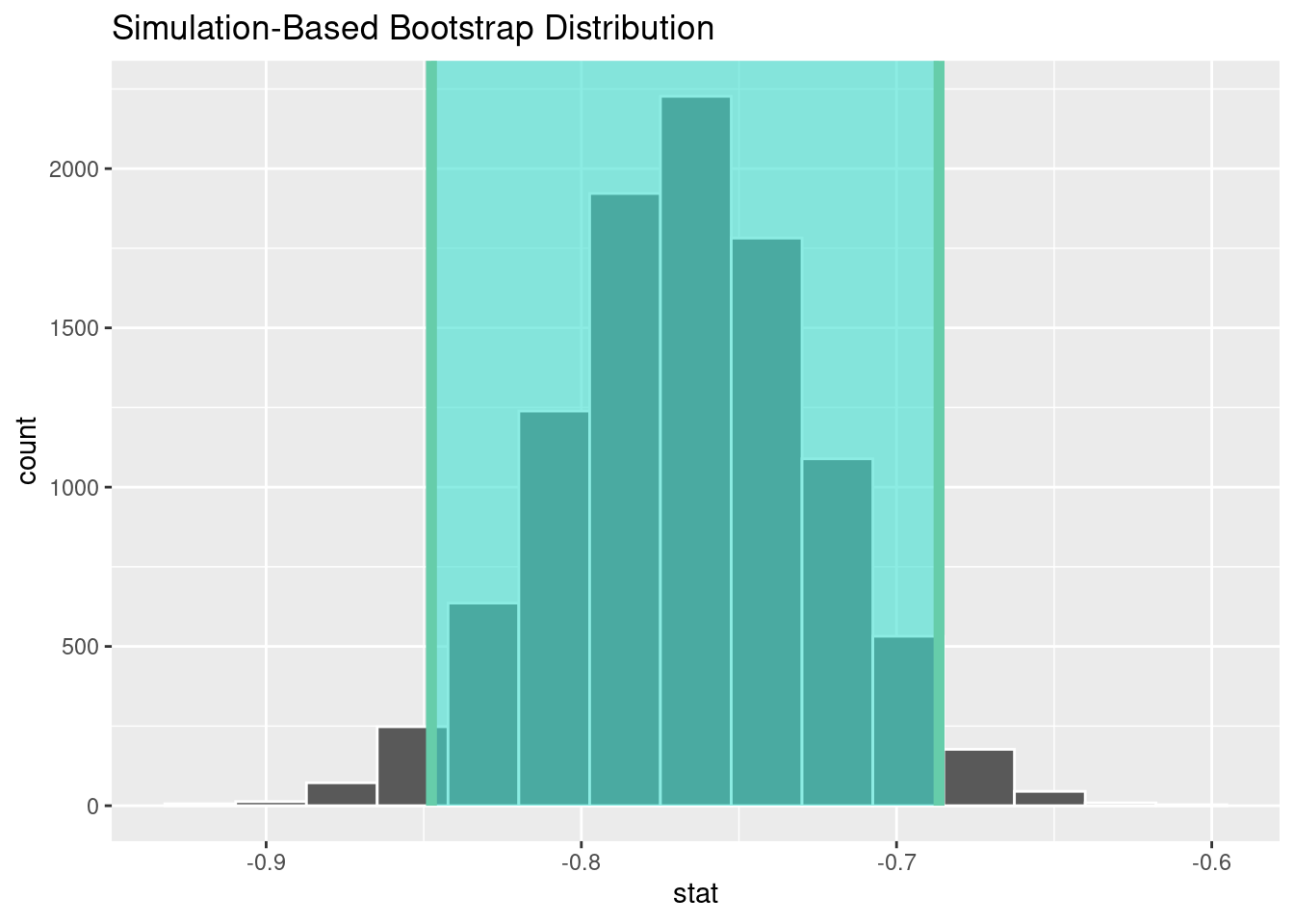
Verglichen mit dem Konfidenzintervall basierend auf der Normalverteilungsannahme, ist Bootstrap hier sehr ähnlich. Das liegt daran, dass die Normalverteilungsannahme und die Homoskedastizitätsannahme ja erfüllt sind. In so einem Fall sind die Standardkonfidenzintervalle basierend auf der Normalverteilungsannahme und dem Bootstrap sehr ähnlich. Wir würden also im Normalfall einfach die Standardkonfidenzintervalle benutzten.
get_regression_table(lin_mod) %>%
filter(term == 'anreise') %>%
kable()| term | estimate | std_error | statistic | p_value | lower_ci | upper_ci |
|---|---|---|---|---|---|---|
| anreise | -0.766 | 0.051 | -14.99 | 0 | -0.867 | -0.665 |
Wir können mit infer auch einen Hypothesentest durchführen, der untersucht, ob die Steigung von Null verschieden ist.
- H\(_0\): \(\beta_1 = 0\)
- H\(_1\): \(\beta_1 \neq 0\)
null_distn_slope <- befragung %>%
specify(formula = zeit_bib ~ anreise) %>%
hypothesize(null = "independence") %>%
generate(reps = 10000) %>%
calculate(stat = "slope")## Setting `type = "permute"` in `generate()`.Für die Darstellung brauchen wir noch die berechnete Steigung:
observed_slope <- befragung %>%
specify(formula = zeit_bib ~ anreise) %>%
calculate(stat = "slope")
observed_slope## Response: zeit_bib (numeric)
## Explanatory: anreise (numeric)
## # A tibble: 1 × 1
## stat
## <dbl>
## 1 -0.766Und nun die Visualisierung:
visualize(null_distn_slope) +
shade_p_value(obs_stat = observed_slope, direction = "both")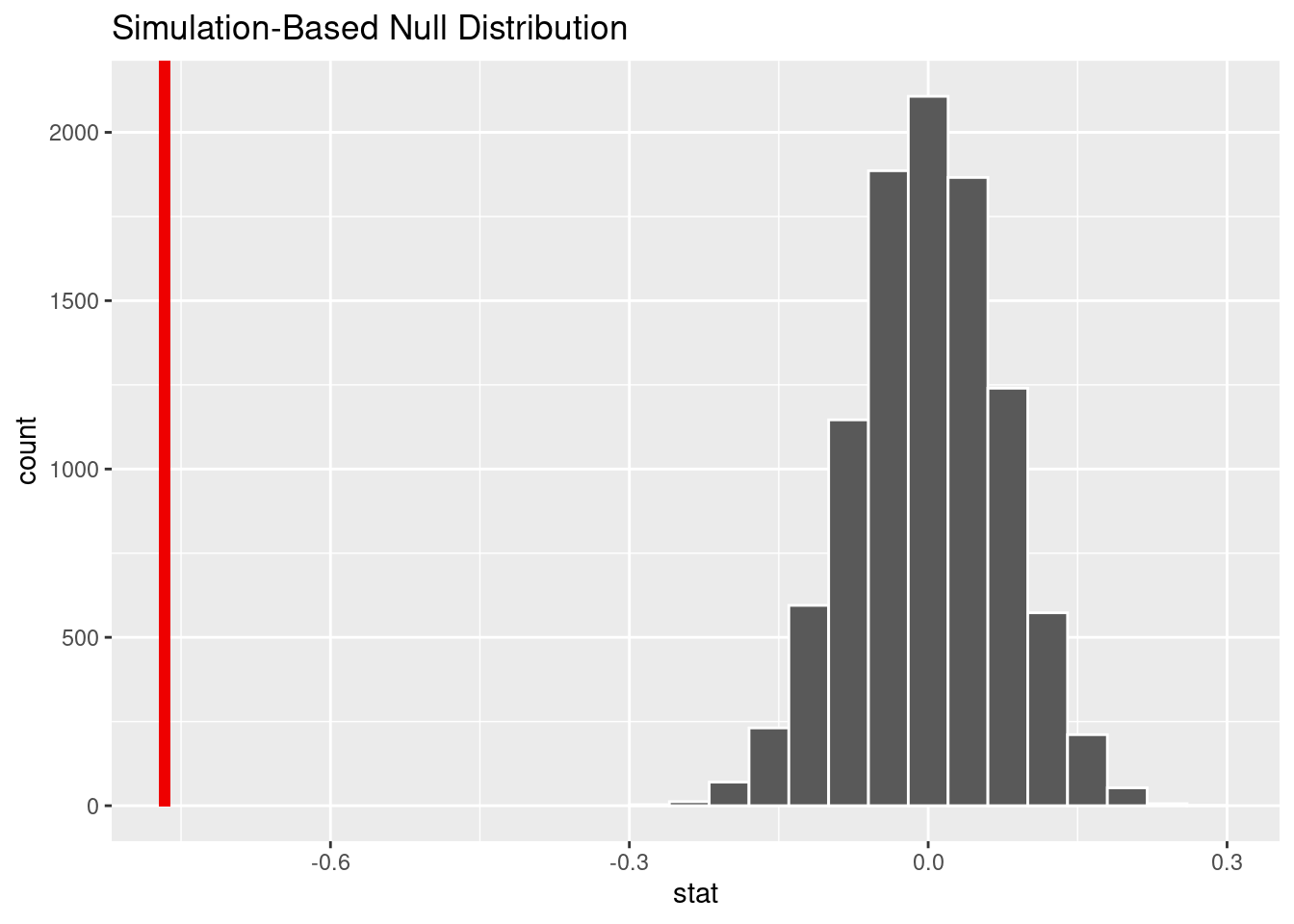
null_distn_slope %>%
get_p_value(obs_stat = observed_slope, direction = "both")## Warning: Please be cautious in reporting a p-value of 0. This result is an
## approximation based on the number of `reps` chosen in the `generate()` step. See
## `?get_p_value()` for more information.## # A tibble: 1 × 1
## p_value
## <dbl>
## 1 0
12.3 Bootstrap mit rsample: Konfidenzintervalle für Steigung und \(y\)-Achsenabschnitt
Falls wir doch Konfidenzintervalle für beide Modellparameter brauchen (und die Annahmen Normalverteilung und/oder Homoskedastizität verletzt sind) oder aber ein lineares Modell mit mehreren Prädiktoren anpassen, können wir nicht mehr mit infer arbeiten. Es gibt aber ein ganzes Modelluniversum, zusammengestellt in der Paketsammlung tidymodels (https://www.tidymodels.org/). Darin gibt es nicht nur alle möglichen Modelle, sondern vor allem eine tidy und einheitliche Herangehensweise ans Modellieren. tidymodels ist jenseits dessen, was wir in diesem Kurs machen werden. Wir werden aber die Bibliothek rsample nutzen, die uns beim Bootstrappen hilft.
Um Konfidenzintervalle sowohl für den \(y\)-Achsenabschnitt als auch für die Steigung zu bekommen, generieren wir Bootstrap-Stichproben aus der befragung, passen dann an jede solche Stichprobe unser lineares Modell an. Jedes dieser Modelle liefert uns einen \(y\)-Achsenabschnitt und eine Steigung. Dadurch bekommen wir Bootstrapverteilungen dieser Modellparameter, so wie sonst auch, wenn wir Bootstrap benutzt haben. Aus diesen Bootstrapverteilungen berechnen wir dann mit der Methode der Quantile unsere Konfidenzintervalle.
Schritt 1: Bootstrapstichproben aus befragung generieren
Wir generieren 10000 Bootstrap-Stichproben aus dem Datensatz befragung mithilfe der Funktion bootstraps() aus der Bibliothek rsample.
set.seed(123)
bootstrap_reps <- 10000
my_bootstraps <- bootstraps(befragung, times = bootstrap_reps)Das Objekt my_bootstraps ist ein “verpacktes” (nested) Objekt. Jeder split ist eine Bootstrap-Stichprobe.
my_bootstraps## # Bootstrap sampling
## # A tibble: 10,000 × 2
## splits id
## <list> <chr>
## 1 <split [200/72]> Bootstrap00001
## 2 <split [200/72]> Bootstrap00002
## 3 <split [200/72]> Bootstrap00003
## 4 <split [200/70]> Bootstrap00004
## 5 <split [200/68]> Bootstrap00005
## 6 <split [200/68]> Bootstrap00006
## 7 <split [200/74]> Bootstrap00007
## 8 <split [200/69]> Bootstrap00008
## 9 <split [200/79]> Bootstrap00009
## 10 <split [200/73]> Bootstrap00010
## # … with 9,990 more rows
class(my_bootstraps)## [1] "bootstraps" "rset" "tbl_df" "tbl" "data.frame"Wir sehen uns so eine Bootstrap-Stichprobe mal an. Dazu nutzen wir die Funktion analysis(), die solche splits richtig behandelt. Jede Bootstrap-Stichprobe ist durch Ziehen mit Zurücklegen aus dem Datensatz befragung hervorgegangen, das ist ja beim Bootstrap immer so.
analysis(my_bootstraps$splits[[1]])## # A tibble: 200 × 7
## # Groups: replicate [1]
## replicate student_id geschlecht wohnort verkehrsmittel anreise zeit_bib
## <int> <int> <chr> <chr> <chr> <dbl> <dbl>
## 1 1 5641 w stadt fahrrad 21.0 304.
## 2 1 4887 w stadt zu_fuss 12.9 303.
## 3 1 2672 w stadt zu_fuss 10.8 313.
## 4 1 2771 m stadt zu_fuss 5.86 286.
## 5 1 8221 w stadt auto 18.2 310.
## 6 1 1236 w stadt zu_fuss 6.51 330.
## 7 1 5395 w stadt bus 25.9 297.
## 8 1 11681 m land bus 109. 245.
## 9 1 2672 w stadt zu_fuss 10.8 313.
## 10 1 5395 w stadt bus 25.9 297.
## # … with 190 more rowsWie viele Studierende wurden mehrfach gezogen? Wir sehen uns als Beispiel die erste Bootstrap-Stichprobe an.
analysis(my_bootstraps$splits[[1]]) %>%
group_by(student_id) %>%
summarise(n = n()) %>%
arrange(desc(n))## # A tibble: 128 × 2
## student_id n
## <int> <int>
## 1 4148 4
## 2 4384 4
## 3 5342 4
## 4 2043 3
## 5 2416 3
## 6 4045 3
## 7 4418 3
## 8 5395 3
## 9 5641 3
## 10 5971 3
## # … with 118 more rowsSchritt 2: Modell auf den Bootstrap-Stichproben anpassen
Um unser ursprüngliches lineares Modell anzupassen, benutzen wir eine selbst geschriebene Funktion, inspiriert von der Hilfe zu rsample (?int_pctl). Die Funktion lm_est() passt auf einer Bootstrap-Stichprobe das lineare Modell zeit_bib ~ anreise an. Um die Berechnung auf allen Bootstrap-Stichproben effizient zu machen, nutze ich die Funktion map(), die sich eine Bootstrap-Stichprobe nach der anderen vornimmt und das lineare Modell anpasst. Wir kommen in einer späteren Stunde auf solche effizienten Funktionen zurück.
lm_est <- function(split, ...) {
lm(zeit_bib ~ anreise, data = analysis(split)) %>%
tidy()
}
model_res <- my_bootstraps %>%
mutate(results = map(splits, .f = lm_est))Wir sehen uns das entstandene Objekt mit allen angepassten Modellen an. Und \(\dots\) wir sehen nichts 😄.
model_res## # Bootstrap sampling
## # A tibble: 10,000 × 3
## splits id results
## <list> <chr> <list>
## 1 <split [200/72]> Bootstrap00001 <tibble [2 × 5]>
## 2 <split [200/72]> Bootstrap00002 <tibble [2 × 5]>
## 3 <split [200/72]> Bootstrap00003 <tibble [2 × 5]>
## 4 <split [200/70]> Bootstrap00004 <tibble [2 × 5]>
## 5 <split [200/68]> Bootstrap00005 <tibble [2 × 5]>
## 6 <split [200/68]> Bootstrap00006 <tibble [2 × 5]>
## 7 <split [200/74]> Bootstrap00007 <tibble [2 × 5]>
## 8 <split [200/69]> Bootstrap00008 <tibble [2 × 5]>
## 9 <split [200/79]> Bootstrap00009 <tibble [2 × 5]>
## 10 <split [200/73]> Bootstrap00010 <tibble [2 × 5]>
## # … with 9,990 more rowsDie Ergebnisse müssen wir noch “auspacken.”
model_coeffs <- model_res %>%
# Die Spalte splits los werden.
select(-splits) %>%
# Und das Ergebnis in ein tibble umwandeln.
unnest(results)
model_coeffs## # A tibble: 20,000 × 6
## id term estimate std.error statistic p.value
## <chr> <chr> <dbl> <dbl> <dbl> <dbl>
## 1 Bootstrap00001 (Intercept) 301. 2.18 138. 1.29e-198
## 2 Bootstrap00001 anreise -0.724 0.0531 -13.7 2.47e- 30
## 3 Bootstrap00002 (Intercept) 302. 2.40 126. 5.25e-191
## 4 Bootstrap00002 anreise -0.781 0.0585 -13.3 2.11e- 29
## 5 Bootstrap00003 (Intercept) 302. 2.21 136. 8.71e-198
## 6 Bootstrap00003 anreise -0.813 0.0506 -16.1 8.94e- 38
## 7 Bootstrap00004 (Intercept) 300. 2.22 135. 5.73e-197
## 8 Bootstrap00004 anreise -0.751 0.0554 -13.6 4.93e- 30
## 9 Bootstrap00005 (Intercept) 299. 2.18 137. 2.89e-198
## 10 Bootstrap00005 anreise -0.742 0.0493 -15.1 1.19e- 34
## # … with 19,990 more rowsJetzt können wir sehen, dass das Objekt model_coeffs die beiden Modellparameter, \(y\)-Achsenabschnitt und die Steigung, enthält und das jeweils so häufig, wie wir eben Bootstrap-Stichproben generiert haben. Somit haben wir jetzt eine Bootstrapverteilung dieser Modellparameter, die wir nun plotten können.
ggplot(model_coeffs, aes(x = estimate, group = term)) +
geom_histogram(col = "white", bins = 30) +
facet_wrap(~ term, scales = "free_x")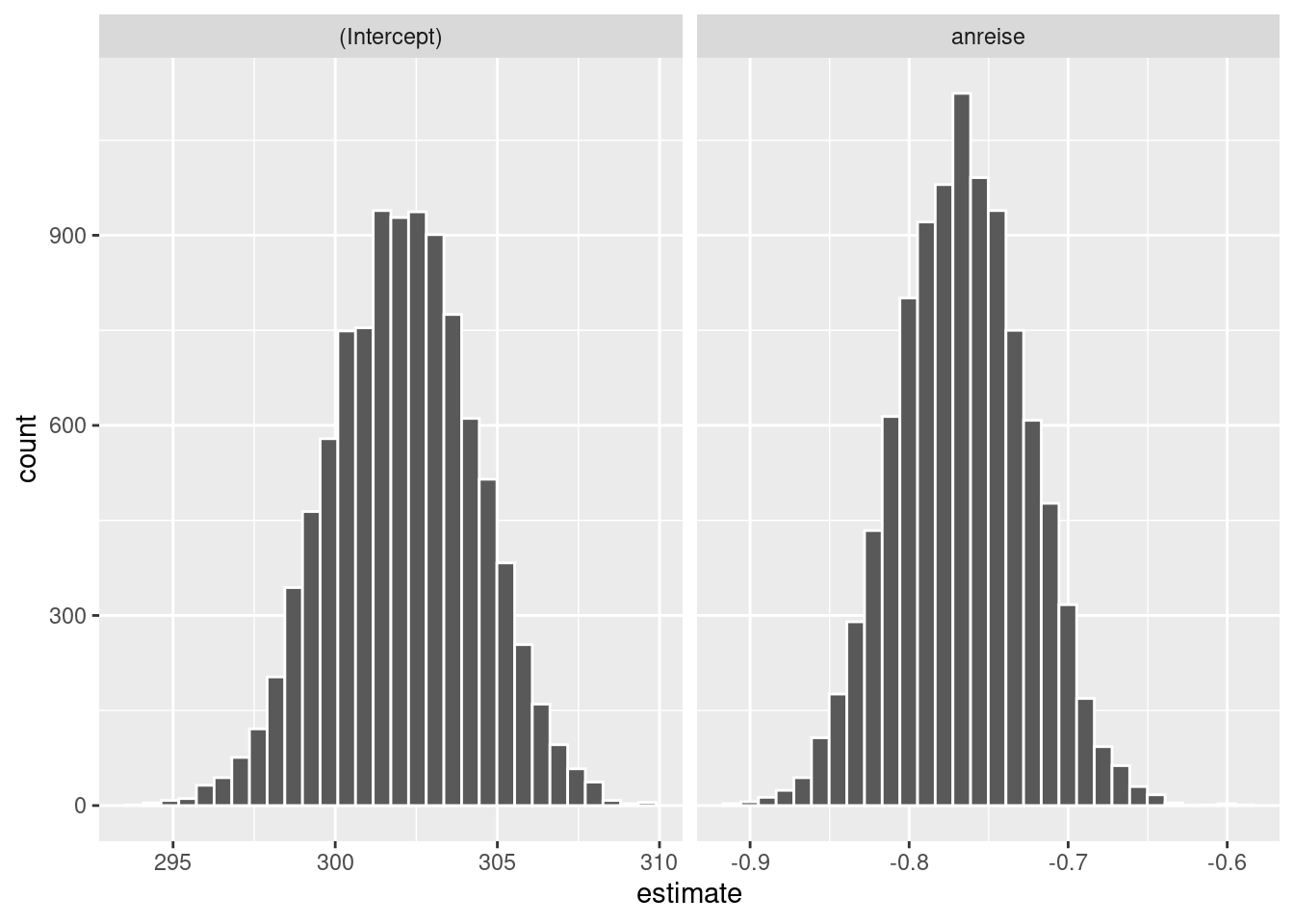
Schritt 3: Konfidenzintervalle berechnen
Die Verteilungen sind symmetrisch, weil ja die Annahmen der Normalregression erfüllt sind. Jetzt fehlen uns noch die Konfidenzintervalle, von denen wir erwarten, dass sie den Standardkonfidenzintervallen ähnlich sein werden.
# Konfidenzintervalle mit Bootstrap
percentile_ci <- int_pctl(model_res, results)
# Standard-Konfidenzintervalle mit der Annahme der Normalverteilung und Homoskedastizität der Residuen
standard_ci <- tidy(lin_mod, conf.int = TRUE)
percentile_ci %>% kable()| term | .lower | .estimate | .upper | .alpha | .method |
|---|---|---|---|---|---|
| (Intercept) | 297.7116451 | 302.0940668 | 306.4549805 | 0.05 | percentile |
| anreise | -0.8462787 | -0.7665325 | -0.6867705 | 0.05 | percentile |
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| (Intercept) | 302.0937700 | 2.2818977 | 132.38708 | 0 | 297.5938278 | 306.5937121 |
| anreise | -0.7662672 | 0.0511189 | -14.98989 | 0 | -0.8670746 | -0.6654598 |
Wir plotten alle Ergebnisse jetzt zusammen. Das müssen wir “händisch” machen, da uns ja nicht die tolle Funktion visualize() aus infer zur Verfügung steht. Wir fügen die Konfidenzintervalle als vertikale Linien zu den Histogrammen der Bootstrapverteilungen hinzu.
ggplot(model_coeffs, aes(x = estimate, group = term)) +
geom_histogram(col = "white", bins = 30) +
geom_vline(data = percentile_ci, aes(xintercept = .lower, group = term, col = 'percentile_ci_lower')) +
geom_vline(data = percentile_ci, aes(xintercept = .upper, group = term), col = 'blue') +
geom_vline(data = standard_ci, aes(xintercept = conf.low, group = term, col = 'conf.low')) +
geom_vline(data = standard_ci, aes(xintercept = conf.high, group = term), col = 'orange') +
scale_color_manual(name = "Confidence intervals", values = c(percentile_ci_lower = "blue", conf.low = 'orange'), labels = c('standard', 'bootstrap')) +
facet_wrap(~ term, scales = "free_x") +
theme(legend.position = 'bottom')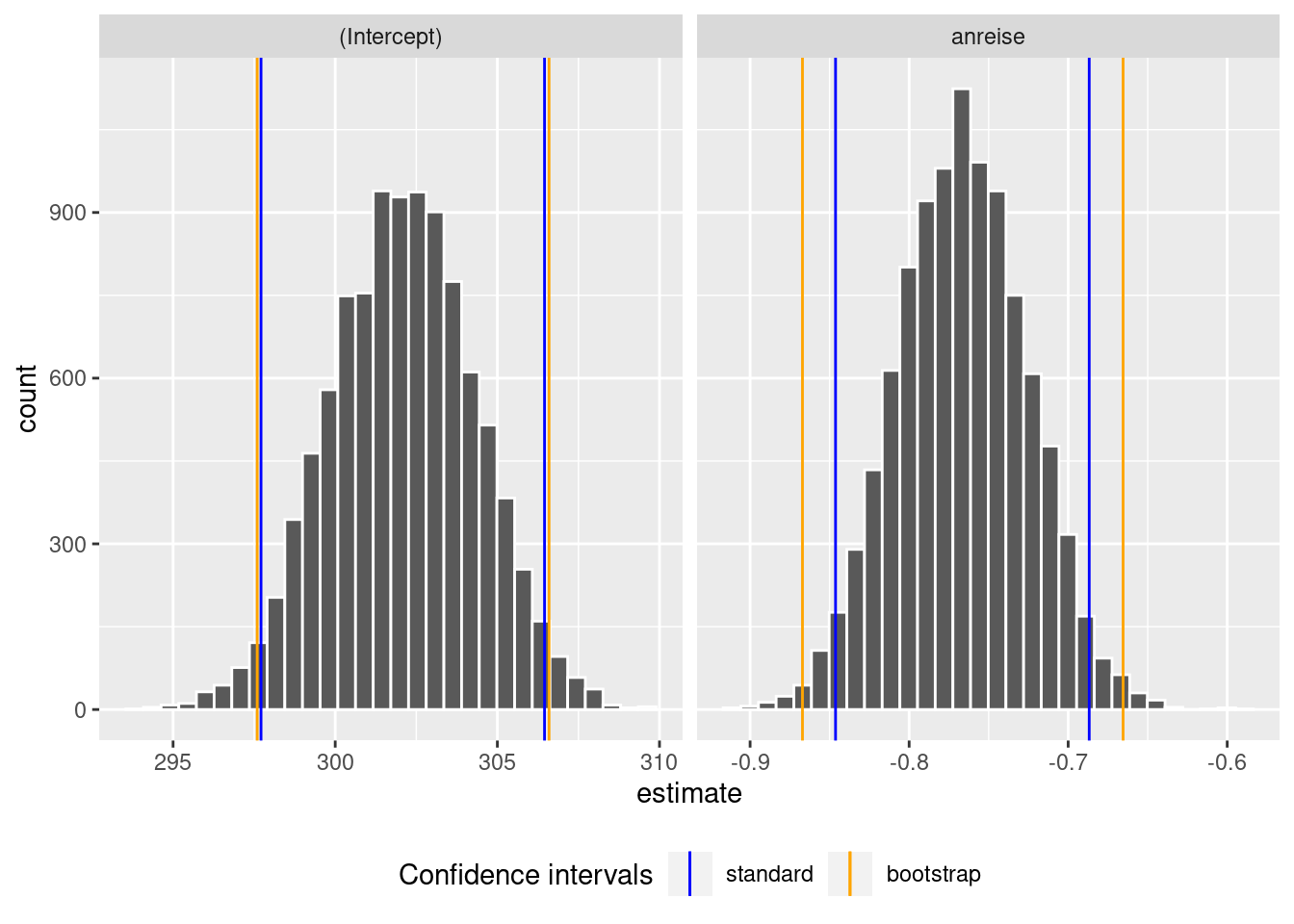
In diesem Beispiel ähneln sich die Konfidenzintervalle, da die Annahmen der Normalregression erfüllt sind. Das wird in den Aufgaben (s.u.), die Sie selbstständig bearbeiten werden, nicht mehr der Fall sein. Selbstverständlich sollen Sie im Falle von erfüllten Annahmen einfach die Standardkonfidenzintervalle nutzen und brauchen kein Bootstrap. Sie werden aber sehen, dass beim Modellieren mit richtigen Daten die Annahmen der Normalverteilung und der Homoskedastizität häufig verletzt sind. Mit dem Bootstrap sind Sie jetzt dafür gerüstet 😄.
12.4 Lesestoff
Kapitel 10 in Ismay and Kim (2021)
12.5 Aufgaben
12.5.1 Artenreichtum auf den Galapagosinseln
Wir beschäftigen uns mit dem Datensatz gala aus der Bibliothek faraway.
- Laden Sie den Datensatz und lesen Sie in der Hilfe nach, um was es sich dabei handelt.
- Untersuchen Sie die Hypothese, dass die Anzahl der endemischen Arten linear von der Gesamtartenzahl abhängt.
- Überprüfen Sie die Annahmen des linearen Modells.
- Vergleichen Sie das Konfidenzintervall, das auf der Normalverteilungsannahme beruht, mit dem Bootstrap-Konfidenzintervall.
- Führen Sie den Hypothesentest analog zum Beispiel oben mit
inferdurch. - Interpretieren Sie das Modell.