Kapitel 7 Stichproben und Variabilität
- Begriffe Stichprobenverteilung und Standardfehler erklären
- Zufall bei wiederholter Stichprobenerhebung erkennen
- Stichprobenverteilung darstellen
- Einfluss der Stichprobengröße auf Stichprobenverteilung benennen
Mit diesem Kapitel steigen wir in die schließende Statistik ein. Wir beginnen damit, wie man in der Statistik zu Daten kommt (Stichprobenerhebung) und welche Rolle der Zufall dabei spielt. Dabei konzentrieren wir uns auf die Erhebung von einfachen zufälligen Stichproben (Zufallsstichproben), nicht auf das Designen von komplizierten Erhebungen. Das ist eine Kunst für sich und geht über die Ziele dieses Kurses hinaus.
7.1 Stichproben
Wir nutzen wieder die selbst erstellten Daten aus der Aufgabe B.1. Die 12000 Studierenden sind unsere Grundgesamtheit. Da wir die Daten selbst erstellt haben, wissen wir alles über sie. Das ist ein großer Vorteil von Computerexperimenten 😄. Damit alle dieselben Daten erstellen, ist die Zeile set.seed(123) notwendig. Sie sorgt dafür, dass der Generator für Zufallszahlen in einen zufälligen, aber reproduzierbaren Zustand versetzt wird. Die Zahl in den Klammern ist nicht wichtig. Wichtig ist, dass alle dieselbe benutzen.
Für bessere Nachvollziehbarkeit, nummerieren wir unsere Studierenden diesmal durch.
set.seed(123)
student_id <- 1:12000
anreise <- c(runif(n = 12000 * 0.8, min = 5, max = 40),
runif(n = 12000 * 0.2, min = 60, max = 120))
geschlecht <- sample(c('m', 'w'), size = 12000, replace = TRUE)
wohnort <- sapply(anreise, function(x) {
if(x < 30) 'stadt'
else 'land'
})
verkehrsmittel <- sapply(anreise, function(x) {
if(x <= 10) 'zu_fuss'
else if(x > 10 & x <= 15) sample(c('zu_fuss', 'fahrrad'), size = 1)
else if(x > 15 & x <= 45) sample(c('bus', 'fahrrad', 'auto'), size = 1)
else sample(c('bus', 'auto'), size = 1)
})
zeit_bib <- 5 * 60 - 0.7 * anreise + rnorm(length(anreise), 0, 20)
grundgesamtheit <- tibble(student_id, geschlecht, wohnort, verkehrsmittel, anreise, zeit_bib)
grundgesamtheit## # A tibble: 12,000 × 6
## student_id geschlecht wohnort verkehrsmittel anreise zeit_bib
## <int> <chr> <chr> <chr> <dbl> <dbl>
## 1 1 w stadt bus 15.1 294.
## 2 2 w land fahrrad 32.6 254.
## 3 3 w stadt fahrrad 19.3 231.
## 4 4 m land auto 35.9 245.
## 5 5 m land bus 37.9 234.
## 6 6 w stadt zu_fuss 6.59 303.
## 7 7 w stadt bus 23.5 284.
## 8 8 m land auto 36.2 274.
## 9 9 m stadt fahrrad 24.3 299.
## 10 10 w stadt bus 21.0 282.
## # … with 11,990 more rowsWir wollen nun 50 Studierende befragen. Durch die zufällige Auswahl an Befragten erzeugen wir eine zufällige Stichprobe. Übersetzt in unser Computerexperiment bedeutet es, dass wir zufällig 50 Zeilen aus dem Datensatz grundgesamtheit ziehen, und zwar so, dass sich diese Zeilen nicht wiederholen (d.h. niemand mehrfach befragt wird). Dazu nutzen wir die Funktion rep_sample_n(), die wiederholt (rep) n Zeilen zieht (sample), und zwar mit der Einstellung replace = FALSE, also ohne Zurücklegen. Wir befragen nur einmal, daher reps = 1.
Damit alle wieder dieselben Daten bekommen, setzen wir vorher den seed (Zustand des Zufallszahlengenerators). Die Variable befragung_size gibt die Stichprobengröße an.
set.seed(345)
befragung_size <- 50
befragung <- rep_sample_n(grundgesamtheit, size = befragung_size, replace = FALSE, reps = 1)
befragung## # A tibble: 50 × 7
## # Groups: replicate [1]
## replicate student_id geschlecht wohnort verkehrsmittel anreise zeit_bib
## <int> <int> <chr> <chr> <chr> <dbl> <dbl>
## 1 1 1623 m stadt zu_fuss 7.06 299.
## 2 1 9171 m stadt fahrrad 11.3 278.
## 3 1 10207 w land bus 107. 199.
## 4 1 3506 w stadt bus 25.0 326.
## 5 1 8892 w stadt bus 28.1 259.
## 6 1 5460 m stadt bus 23.6 299.
## 7 1 6120 w stadt bus 20.0 268.
## 8 1 865 w stadt fahrrad 26.6 290.
## 9 1 11586 m land bus 114. 207.
## 10 1 8153 w stadt zu_fuss 8.06 297.
## # … with 40 more rowsDie Variable replicate zeigt immer 1. Das bedeutet, dass wir die Befragung einmal wiederholt (repliziert) haben und alle Datenpunkte zu dieser Wiederholung gehören.
Wir wollen nun wissen, wie viele Studierende unter den Befragten in der Stadt oder auf dem Land wohnen.
## # A tibble: 2 × 2
## # Groups: wohnort [2]
## wohnort n
## <chr> <int>
## 1 land 21
## 2 stadt 29Das Ganze möchten wir als Anteile ausdrücken. Die Funktion n() kann innerhalb der Funktion summarise() zum Auszählen genutzt werden. Wir teilen durch die Stichprobengröße.
## # A tibble: 2 × 2
## wohnort prop
## <chr> <dbl>
## 1 land 0.42
## 2 stadt 0.58Es wohnen also 42% auf dem Land und 58% in der Stadt.
Was passiert, wenn wir die Befragung mehrfach wiederholen, sagen wir 33 Mal? In der Realität ist dieses Szenario sehr unwahrscheinlich, aber in einem Computerexperiment einfach zu implementieren. Es hilft uns ein Gefühl für die Variabilität, die durch das zufällige Auswählen der Studierenden bei der Befragung entsteht, zu entwickeln.
Wir setzten erneut den seed, damit alle dieselben Ergebnisse bekommen.
set.seed(234)
befragung_reps <- rep_sample_n(grundgesamtheit, size = befragung_size, replace = FALSE, reps = 33)
befragung_reps## # A tibble: 1,650 × 7
## # Groups: replicate [33]
## replicate student_id geschlecht wohnort verkehrsmittel anreise zeit_bib
## <int> <int> <chr> <chr> <chr> <dbl> <dbl>
## 1 1 2079 m land auto 38.8 262.
## 2 1 1314 m stadt fahrrad 13.3 301.
## 3 1 1710 m stadt auto 26.5 272.
## 4 1 4386 w stadt bus 23.9 269.
## 5 1 9490 m land auto 34.2 262.
## 6 1 11757 w land bus 102. 227.
## 7 1 11649 w land bus 111. 202.
## 8 1 2244 m land bus 38.9 256.
## 9 1 3652 w stadt fahrrad 10.3 254.
## 10 1 3127 m stadt fahrrad 29.6 271.
## # … with 1,640 more rowsJetzt wird uns angezeigt, dass es in dem Datensatz befragung_reps 33 replicates (Wiederholgungen) gibt. Diese sind einfach nacheinander in befragung_reps angeordnet (blättern Sie durch den Datensatz). Dementsprechend hat der Datensatz 50 \(\times\) 33 = 1650 Zeilen.
Wie sieht es jetzt mit den Anteilen von Stadt- und Landbewohnern aus? Wir müssen nun zusätzlich zum wohnort auch noch nach replicate gruppieren.
wohnort_props <- befragung_reps %>%
group_by(replicate, wohnort) %>%
summarise(prop = n()/befragung_size)
wohnort_props## # A tibble: 66 × 3
## # Groups: replicate [33]
## replicate wohnort prop
## <int> <chr> <dbl>
## 1 1 land 0.42
## 2 1 stadt 0.58
## 3 2 land 0.36
## 4 2 stadt 0.64
## 5 3 land 0.4
## 6 3 stadt 0.6
## 7 4 land 0.38
## 8 4 stadt 0.62
## 9 5 land 0.4
## 10 5 stadt 0.6
## # … with 56 more rowsErwartungsgemäß bringt jede Wiederholung der Befragung, die wir ja als zufälliges Herausgreifen der Studierenden ohne Mehrfachbefragung programmiert haben, etwas andere Ergebnisse. Sehen Sie sich die student_id in den replicates an, es werde unterschiedliche Studierende befragt! In einem Histogramm sieht das Ganze so aus:
ggplot(data = wohnort_props, aes(x = prop)) +
geom_histogram(binwidth = 0.05, boundary = 0.4, col = 'white') +
facet_wrap(~ wohnort) +
labs(x = 'Anteile beim Wohnort', title = 'Verteilung der Wohnorte', y = 'Häufigkeit')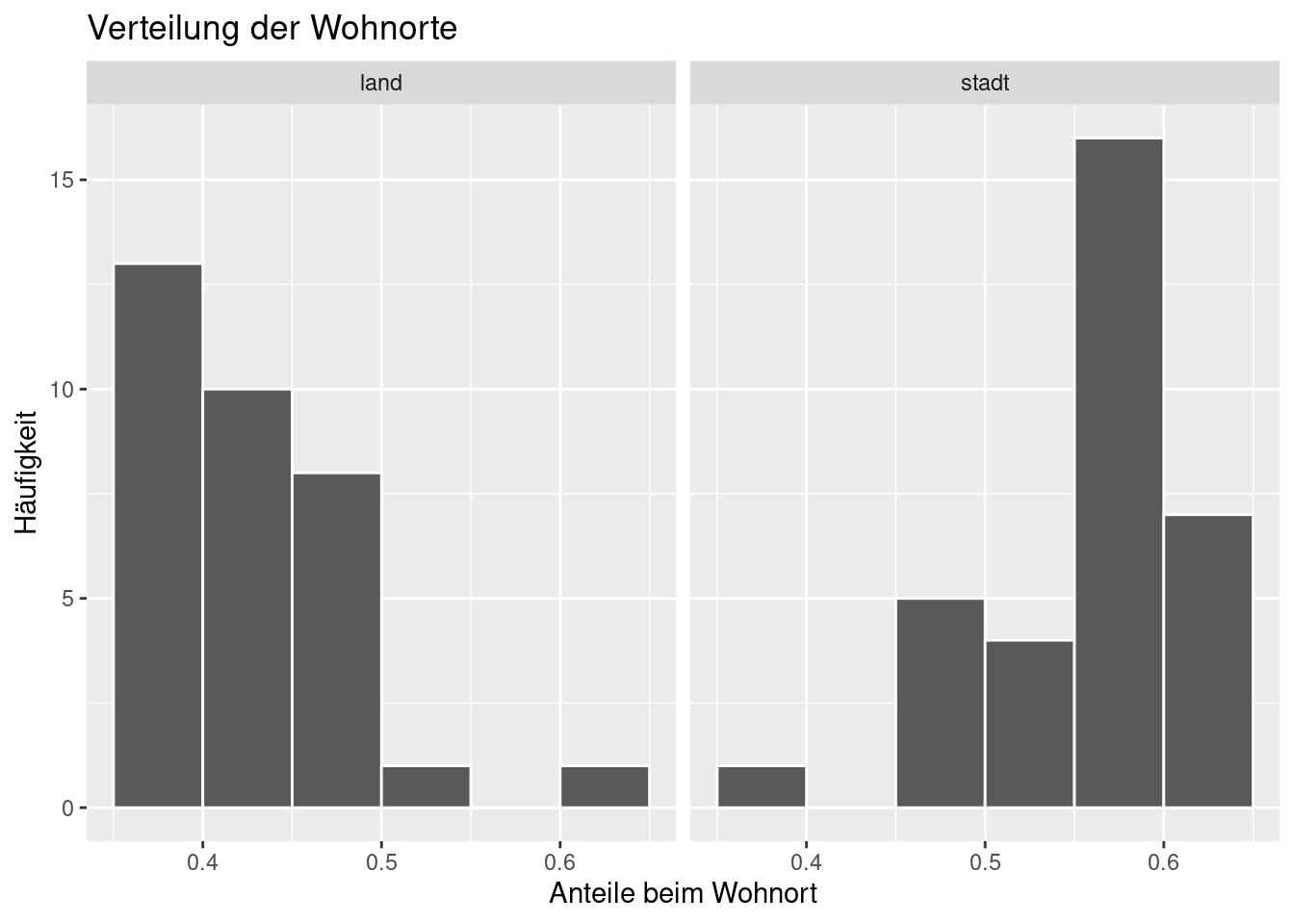
Die häufigsten Anteile sind um die 40% für Land und um die 60% für Stadt. Wir können es sogar etwas genauer ablesen, da wir binwidth = 0.05 gewähnt haben, also Schritte von 5%. Es sind 35–40% für Land und 55–60% für Stadt.
7.2 Anzahl der Wiederholungen und Variabilität
Was passiert, wenn wir unsere Umfrage 1000 Mal wiederholen? Wir können den ganzen Code wiederverwenden und müssen nur die reps entsprechend verändern. Wir erstellen dafür eine zusätzliche Variable befragung_num. Beim Histogramm sollten wir die binwidth etwas heruntersetzten, da wir jetzt sehr viel mehr Daten haben und diese detaillierter anzeigen lassen können. Zusätzlich wird die x-Achse “frei” gegeben, i.e. die Skalierung wird jetzt auf jeder Achse separat bestimmt scales = 'free_x' in facet_wrap(), um die Verteilungen besser zu sehen.
set.seed(345)
befragung_num <- 1000
befragung_reps <- rep_sample_n(grundgesamtheit, size = befragung_size, replace = FALSE, reps = befragung_num)
wohnort_props <- befragung_reps %>%
group_by(replicate, wohnort) %>%
summarise(prop = n()/befragung_size)
ggplot(data = wohnort_props, aes(x = prop)) +
geom_histogram(binwidth = 0.02, boundary = 0.4, col = 'white') +
facet_wrap(~ wohnort, scales = 'free_x') +
labs(x = 'Anteile beim Wohnort', title = 'Verteilung der Wohnorte', y = 'Häufigkeit')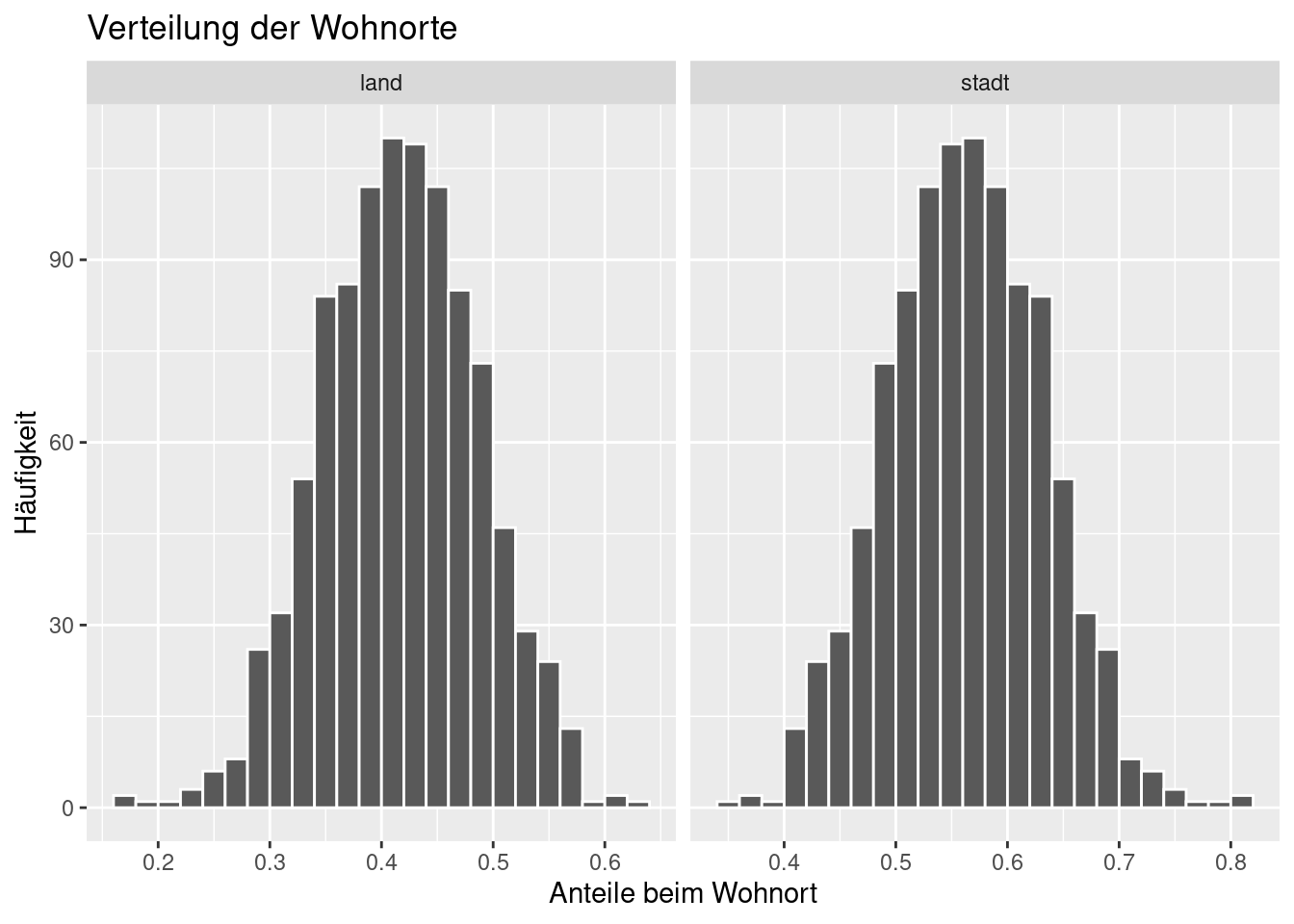
Die häufigsten Anteile beim Land liegen bei 40–42% und bei der Stadt bei 58–60%.
Die Histogramme geben nun gut die Verteilung der Anteile der Stadt- und Landbewohner wieder. Solche Verteilungen nennt man Stichprobenverteilungen. Sie zeigen die Verteilung einer statistischen Kenngröße (Statistik), in unserem Fall Anteil, die aus zufälligen Stichproben ausgerechnet wurde. Die Stichprobenverteilung beantwortet die Frage: Wenn ich eine zufällige Menge (Stichprobengröße) an Daten (Zufallsstichprobe) aus der Grundgesamtheit herausgreife und eine Kenngröße (z.B. Anteil) berechne, welchen Wert werde ich im Mittel erhalten und wie stark wird der Wert schwanken.
7.3 Stichprobengröße
Was passiert, wenn wir die Größe der Stichproben variieren? Das würde Befragungen mit unterschiedlicher Anzahl von Teilnehmern entsprechen. Wir vergleichen 25, 50 und 100 Befragte und wiederholen jeweils 1000 Mal, um erneut Stichprobenverteilungen plotten zu können. Das ist eine repetitive Aufgabe und ich werde dafür eine Funktion definieren. Wie man das macht, wird in einer späteren Stunde erklärt.
calculate_props <- function(grund_data = grundgesamtheit, befragung_size, befragung_reps = 1000) {
befragung <- rep_sample_n(grund_data, size = befragung_size, replace = FALSE, reps = befragung_reps)
wohnort_props <- befragung %>%
group_by(replicate, wohnort) %>%
summarise(prop = n()/befragung_size)
wohnort_props
}Nun wenden wir diese selbst definierte Funktion an und führen die Befragungen durch.
set.seed(123)
# Stichprobengröße 25
wohnort_props_25 <- calculate_props(grund_data = grundgesamtheit, befragung_size = 25, befragung_reps = 1000)
# Stichprobengröße 50
wohnort_props_50 <- calculate_props(grund_data = grundgesamtheit, befragung_size = 50, befragung_reps = 1000)
# Stichprobengröße 100
wohnort_props_100 <- calculate_props(grund_data = grundgesamtheit, befragung_size = 100, befragung_reps = 1000)Wir stellen die drei Stichprobenverteilungen dar. Die Einstellung für binwidth ist jeweils eine andere.
ggplot(data = wohnort_props_25, aes(x = prop)) +
geom_histogram(binwidth = 0.04, boundary = 0.4, col = 'white') +
facet_wrap(~ wohnort, scales = 'free_x') +
labs(x = 'Anteile beim Wohnort', title = 'Verteilung der Wohnorte, Stichprobengröße = 25', y = 'Häufigkeit')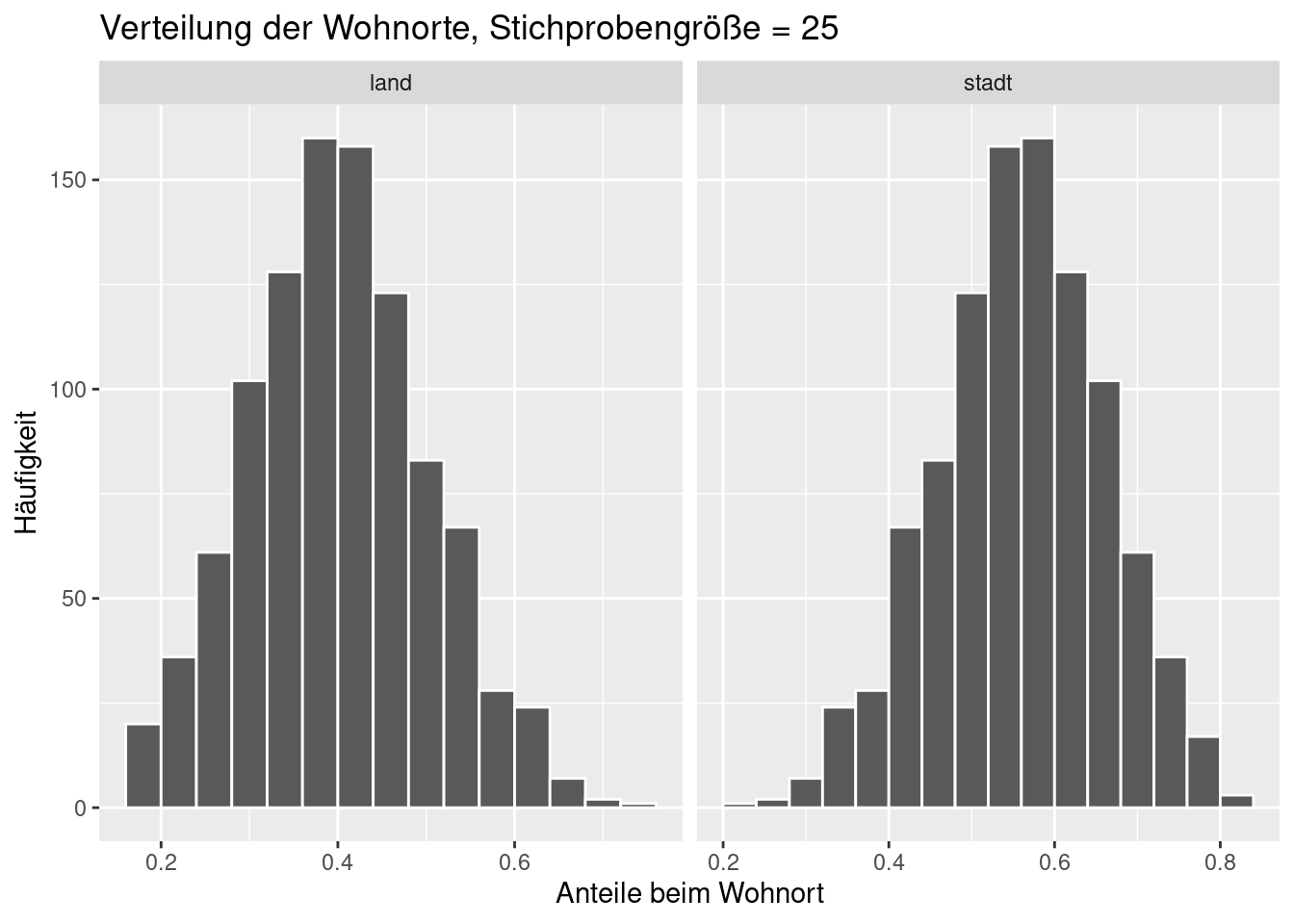
ggplot(data = wohnort_props_50, aes(x = prop)) +
geom_histogram(binwidth = 0.02, boundary = 0.4, col = 'white') +
facet_wrap(~ wohnort, scales = 'free_x') +
labs(x = 'Anteile beim Wohnort', title = 'Verteilung der Wohnorte, Stichprobengröße = 50', y = 'Häufigkeit')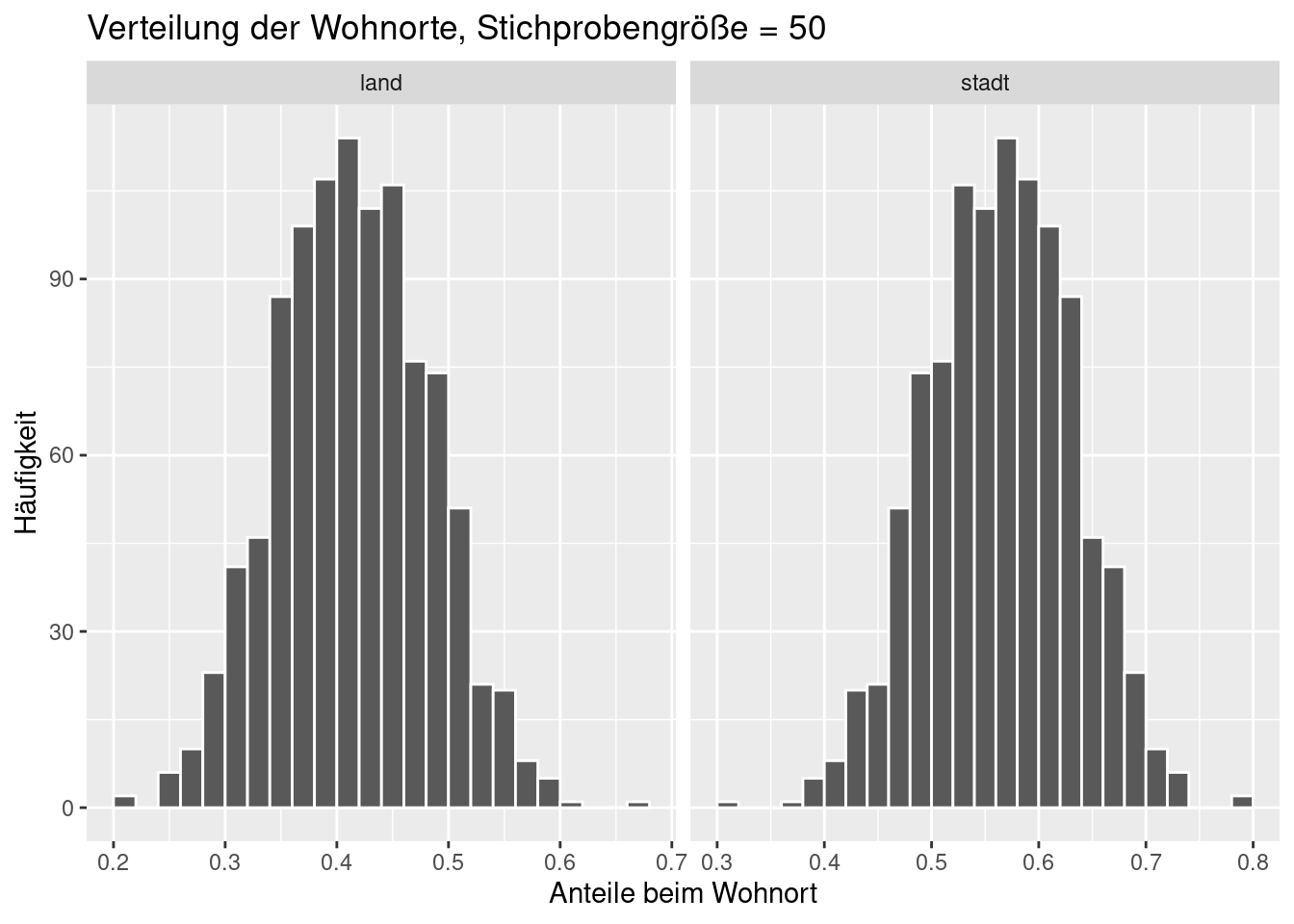
ggplot(data = wohnort_props_100, aes(x = prop)) +
geom_histogram(binwidth = 0.02, boundary = 0.4, col = 'white') +
facet_wrap(~ wohnort, scales = 'free_x') +
labs(x = 'Anteile beim Wohnort', title = 'Verteilung der Wohnorte, Stichprobengröße = 100', y = 'Häufigkeit')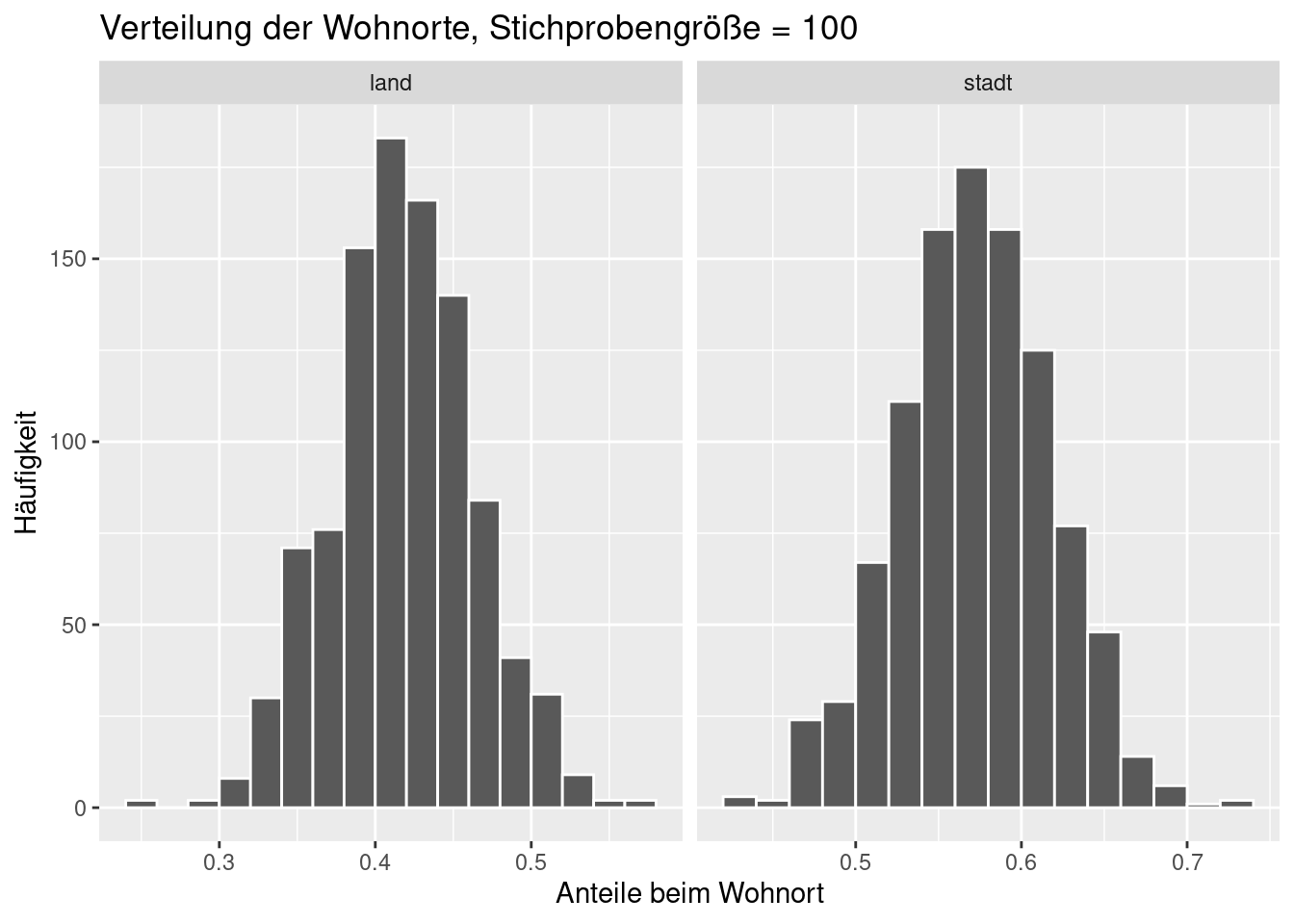
Wie kann man diese Stichprobenverteilungen charakterisieren? Es sind in erster Linie Daten und wie bei jedem Datensatz kann man auch hier einen Mittelwert und eine Standardabweichung angeben. Die Standardabweichung der Stichprobenverteilung heißt Standardfehler und fasst den Einfluss der Variabilität (zufälliges Herausgreifen der Studierenden) zusammen.
## # A tibble: 2 × 2
## wohnort prop_sd
## <chr> <dbl>
## 1 land 0.102
## 2 stadt 0.102## # A tibble: 2 × 2
## wohnort prop_sd
## <chr> <dbl>
## 1 land 0.0679
## 2 stadt 0.0679## # A tibble: 2 × 2
## wohnort prop_sd
## <chr> <dbl>
## 1 land 0.0458
## 2 stadt 0.0458Sie sehen, dass mit steigender Stichprobengröße der Standardfehler sinkt. Das ist intuitiv verständlich, denn je mehr Studierende wir (pro Wiederholung!) befragen, desto repräsentativer ist die Stichprobe.
Da dieses Kapitel so wichtig ist, gibt es ausnahmsweise vorformulierte Take-Home-Messages 😄:
- Eine zufällige Stichprobe ist (meistens\(^*\)) der Königsweg, um repräsentative Informationen über die Grundgesamtheit zu bekommen.
- Die Verteilung einer statistischen Kenngröße, die aus Zufallsstichproben ausgerechnet wurde, heißt Stichprobenverteilung. Um diese Verteilung zu bekommen, muss man wiederholt Stichproben erheben. Je mehr Stichproben man erhebt, desto genauer kann man die Stichprobenverteilung beschreiben.
- Die Standardabweichung der Kenngröße, die durch die Stichprobenverteilung dargestellt wird, heißt Standardfehler.
- Der Zufall macht sich durch eine Streuung (erfasst durch den Standardfehler) in der Stichprobenverteilung bemerkbar. Je größer die einzelnen Stichproben, desto kleiner der Standardfehler.
\(^*\): Manchmal ist die interessierte Größe in unterschiedlichen Untergruppen der Grundgesamtheit unterschiedlich verteilt. Z.B. könnten bestimmte Haltungen in der Bevölkerung gegenüber irgendwelchen Sachverhalten von Alter oder Bildungsstand oder Wohnort (Stadt vs. Land) abhängen. Dann sollte man sich überlegen, ob man statt einer zufälligen Stichprobe lieber eine geschichtete Zufallsstichprobe zieht, d.h. innerhalb dieser Kategorien zufällig beprobt.
7.4 Lesestoff
Kapitel 7 in Ismay and Kim (2021)
7.5 Aufgaben
7.5.1 Wahrer Wert in der Grundgesamtheit
Berechnen Sie die Anteile von Studierenden in der Grundgesamtheit, die in der Stadt bzw. auf dem Land leben. Wie gut waren die Schätzungen im Vergleich zum wahren Wert in der Grundgesamtheit?
7.5.2 Lohnt eine Station zum Ausleihen von Fahrrädern?
In unserem fiktiven Beispiel der Uni Werdeschlau geht es eigentlich darum, ob sich eine Station zum Parken und Reparieren (also eine Servicestation) von Fahrrädern lohnen würde. Daher ist die Frage interessant, wie viele Studierende mit dem Fahrrad zur Uni kommen. Wiederholen Sie die obige Analyse und ermitteln Sie statt der Anteile von Stadt- und Landbewohnern nun die Anteile der unterschiedlichen Verkehrsmittel. Die selbst definierte Funktion müssen Sie durch die folgende ersetzen.
calculate_props_verkehr <- function(grund_data = grundgesamtheit, befragung_size, befragung_reps = 1000) {
befragung <- rep_sample_n(grund_data, size = befragung_size, replace = FALSE, reps = befragung_reps)
verkehrsmittel_props <- befragung %>%
group_by(replicate, verkehrsmittel) %>%
summarise(prop = n()/befragung_size)
verkehrsmittel_props
}In der Lösung zu dieser Aufgabe erhalten Sie auch weitere Tipps zur Darstellung von Histogrammen und Dichtefunktionen 😎.