Kapitel 11 Lineare Regression
- allgemeinen Aufbau eines Regressionsmodells erklären
- Annahmen der linearen Normalregression benennen
- einfache lineare Regression selbst in R durchführen
In diesem Kapitel werden wir in die statistische Modellierung einsteigen. Bisher haben Sie gelernt, wie man mithilfe von modernen Resamplingverfahren oder Simulationen Hypothesentests durchführt und Konfidenzintervalle berechnet. Wir werden in späteren Kapiteln auch für die Modellierung Bootstrap verwenden.
Es gibt im Wesentlichen zwei Gründe, warum man modelliert.
- Wir vermuten einen Zusammenhang zwischen Variablen und wollen diesen überprüfen (explikatives Modellieren).
- Wir wollen ein Modell zur Vorhersage entwickeln (prädiktives Modellieren).
Wir werden uns in diesem Kurs nur mit dem explikativen (erklärenden) Modellieren beschäftigen.
11.1 Begriff Regression
Woher kommt der Begriff Regression? Diesen prägte Sir Francis Galton (1822-1911) (Fahrmeir, Kneib, and Lang 2009). Galton interessierte sich unter anderem für den Zusammenhang zwischen der durchschnittlichen Körpergröße der Eltern und der Körpergröße ihrer erwachsenen Kinder. Leider war er nicht nur einer der Väter der Statistik, sondern auch ein Rassist.
Galton stellte fest, dass Kinder von unterdurchschnittlich kleinen Eltern eher größer waren und umgekehrt, Kinder von überdurchschnittlich großen Eltern eher kleiner waren. Diesen Effekt nannte er Regression (Rückkehr) zur Mitte.
11.2 Idee der Regression
Die Regression ist ein Modell, dass einen Zusammenhang zwischen Variablen analysiert. Wenn dieser Zusammenhang linear ist, dann nennt man das Modell lineare Regression. Wir werden uns ausschließlich mit solchen linearen Modellen beschäftigen.
Die lineare Regression untersucht also den linearen Zusammenhang zwischen den sogen. erklärenden Variablen und der Zielvariablen. Im historischen Beispiel von Galton gab es nur eine erklärende Variable, nämlich die Durchschnittsgröße der Eltern. Die Zielvariable war die zu erwartende Größe der Kinder. Es ging also nicht darum, die exakte Größe eines bestimmten Kindes zu berechnen, sondern den Einfluss der Durchschnittsgröße der Eltern auf die zu erwartende Größe der Kinder. Es ging also um den systematischen Einfluss, nicht um bestimmte Eltern-Kind-Paare. Diese waren nur Stichproben. Spätestens hier sollte es klingeln, denn die Größe der Kinder ist somit eine Zufallsvariable.
Die Zielvariable muss nicht immer stetig wie die Körpergröße sein. Sie kann binär, kategorial oder eine Zählvariable sein. Auch die erklärenden Variablen können stetig, binär oder kategorial sein. Das macht die Regessionsmodelle sehr divers. Wir werden uns im Wesentlichen mit numerischen Zielvariablen beschäftigen.
Wir können somit die Regression so zusammenfassen:
Die Regression ist ein Modell der Form
\[y = f(X) + \varepsilon\]
- \(y\): Zielvariable
- \(f\): Art des Zusammenhangs
- \(X\): Prädiktoren (erklärende Variablen auch Kovariablen)
- \(\varepsilon\): Fehlerterm
Wenn:
- \(f\) linear ist (Einfluss der Prädiktoren addiert sich), spricht man von linearer Regression
- \(X\) nur ein Prädiktor ist, spricht man von einfacher Regression, sonst von multipler Regression
Modellkomponenten:
- \(f(X)\): systematische oder deterministische Komponente
- \(\varepsilon\): stochastische Komponente (Störgröße, Fehlerterm)
Es geht bei der Regression also darum, die systematische Komponente zu modellieren. Der Zusammenhang zwischen Prädiktoren und der Zielvariablen ist nie exakt, es gibt also einen Fehlerterm. Die Zielgröße ist eine Zufallsvariable, deren Verteilung von den Prädiktoren abhängt.
11.3 Einfache lineare Regression
Bei einer einfachen linearen Regression gibt es nur einen Prädiktor. Der Zusammenhang zwischen der Zielvariablen und diesem Prädiktor ist linear. Somit hat das Model die Form einer Geraden. Eine Gerade kann man ja mithilfe des \(y\)-Achsenabschnitts und der Steigung beschreiben. Und genauso sieht das einfache lineare Regressionsmodell aus.
Gegeben sind Datenpaare: \((y_i,x_i), \quad i=1,\dots,n\) zu metrischen Variablen \(y\) und \(x\).
Das Modell \[y_i=\beta_0 + \beta_1x_i + \varepsilon_i, \qquad i=1,\dots,n.\] heißt einfaches lineares Regressionsmodell, wenn die Fehler \(\varepsilon_1,\dots, \varepsilon_n\) unabhängig und identisch verteilt sind (iid) mit
\[\mathrm{E}(\varepsilon_i) = 0, \qquad \mathrm{Var}(\varepsilon_i)=\sigma^2.\] Wenn zusätzlich gilt \[\varepsilon_i \sim N(0,\sigma^2)\] d.h. die Residuen normalverteilt sind, sprechen wir von klassischer Normalregression.
\(\beta_0\) heißt \(y\)-Achsenabschnitt und \(\beta_1\) Steigung des Modells.
\(\varepsilon_i\) steht für Fehler, die wir im Modell machen. Das sind die Unterschiede, genannt Residuen, zwischen dem, was das Modell in dem systematischen Teil (Geradengleichung) \(\beta_0 + \beta_1x_i\) ausrechnet und dem tatsächlich gemessenen Wert \(y_i\).
\(\mathrm{E}\) steht für Erwartungswert. So nennt man den theoretischen Mittelwert einer Zufallsvariablen. Und \(\mathrm{Var}\) steht für Varianz. Beim einfachen linearen Regressionsmodell nimmt man also an, dass die Fehler im Mittel Null sind. Sie werden natürlich nie alle Null sein, sondern sie werden variieren. Der Fehlerterm ist also eine Zufallsvariable, dessen Varianz fest sein soll. Eine feste Varianz nennt man Homoskedastizität und die Fehler entsprechend homoskedastisch. Eine Varianz, die schwankt, bezeichnet man als Heteroskedastizität. Das bedeutet unter anderem, dass die Fehler für kleine und große Werte im Modell ähnlich sein müssen. Um auf Galtons Beispiel zurückzukommen, das Modell soll sowohl die Größe der großen als auch der kleinen Kinder gleich gut erklären.
11.4 Beispiel: Zusammenhang zwischen der Anreisezeit und der Arbeitszeit in der Bibliothek
Als Beispiel für eine einfache lineare Regression nutzen wir wieder unsere simulierten Daten. Zunächst laden wir die Bibliotheken. Die Bibliothek kntir brauchen wir für das Layouten der Tabellen.
Wir generieren wieder unsere Lieblingsgrundgesamtheit.
set.seed(123)
student_id <- 1:12000
anreise <- c(runif(n = 12000 * 0.8, min = 5, max = 40),
runif(n = 12000 * 0.2, min = 60, max = 120))
geschlecht <- sample(c('m', 'w'), size = 12000, replace = TRUE)
wohnort <- sapply(anreise, function(x) {
if(x < 30) 'stadt'
else 'land'
})
verkehrsmittel <- sapply(anreise, function(x) {
if(x <= 10) 'zu_fuss'
else if(x > 10 & x <= 15) sample(c('zu_fuss', 'fahrrad'), size = 1)
else if(x > 15 & x <= 45) sample(c('bus', 'fahrrad', 'auto'), size = 1)
else sample(c('bus', 'auto'), size = 1)
})
zeit_bib <- 5 * 60 - 0.7 * anreise + rnorm(length(anreise), 0, 20)
grundgesamtheit <- tibble(student_id, geschlecht, wohnort, verkehrsmittel, anreise, zeit_bib)
datatable(grundgesamtheit, options = list(scrollX = T)) %>%
formatRound(c('zeit_bib', 'anreise'), 1)Und befragen 200 Studierende.
set.seed(345)
befragung_size <- 200
befragung <- rep_sample_n(grundgesamtheit, size = befragung_size, replace = FALSE, reps = 1)
datatable(befragung, options = list(scrollX = T)) %>%
formatRound(c('zeit_bib', 'anreise'), 1)11.4.1 Modell anpassen
Wir unterstellen einen linearen Zusammenhang zwischen zeit_bib und anreise und passen ein lineares Modell an. Dazu nutzen wir die Funktion lm(). Sie braucht die Zielvariable und den Prädiktor, die Sie mit Tilde verbunden angeben. Das ist die sogen. formula (Formel, so ähnlich wie eine Matheformel). Die Tilde hatten wir schon so ähnlich bei der Bibliothek infer benutzt. Außerdem müssen wir noch den Datensatz, in dem die Variablen zu finden sind, benennen.
lin_mod <- lm(zeit_bib ~ anreise, data = befragung)11.4.2 Modellergebnisse ansehen
Die Struktur eines solchen linearen Modellobjekts ist richtig kompliziert. Daher gibt es verschiedene Methoden, um aus diesem Objekt sinnvolle Information zu entnehmen.
str(lin_mod)## List of 12
## $ coefficients : Named num [1:2] 302.094 -0.766
## ..- attr(*, "names")= chr [1:2] "(Intercept)" "anreise"
## $ residuals : Named num [1:200] 2.55 -15.31 -21.32 42.64 -21.19 ...
## ..- attr(*, "names")= chr [1:200] "1" "2" "3" "4" ...
## $ effects : Named num [1:200] -3903 -312.5 -24.2 42.7 -21.2 ...
## ..- attr(*, "names")= chr [1:200] "(Intercept)" "anreise" "" "" ...
## $ rank : int 2
## $ fitted.values: Named num [1:200] 297 293 220 283 281 ...
## ..- attr(*, "names")= chr [1:200] "1" "2" "3" "4" ...
## $ assign : int [1:2] 0 1
## $ qr :List of 5
## ..$ qr : num [1:200, 1:2] -14.1421 0.0707 0.0707 0.0707 0.0707 ...
## .. ..- attr(*, "dimnames")=List of 2
## .. .. ..$ : chr [1:200] "1" "2" "3" "4" ...
## .. .. ..$ : chr [1:2] "(Intercept)" "anreise"
## .. ..- attr(*, "assign")= int [1:2] 0 1
## ..$ qraux: num [1:2] 1.07 1.05
## ..$ pivot: int [1:2] 1 2
## ..$ tol : num 1e-07
## ..$ rank : int 2
## ..- attr(*, "class")= chr "qr"
## $ df.residual : int 198
## $ xlevels : Named list()
## $ call : language lm(formula = zeit_bib ~ anreise, data = befragung)
## $ terms :Classes 'terms', 'formula' language zeit_bib ~ anreise
## .. ..- attr(*, "variables")= language list(zeit_bib, anreise)
## .. ..- attr(*, "factors")= int [1:2, 1] 0 1
## .. .. ..- attr(*, "dimnames")=List of 2
## .. .. .. ..$ : chr [1:2] "zeit_bib" "anreise"
## .. .. .. ..$ : chr "anreise"
## .. ..- attr(*, "term.labels")= chr "anreise"
## .. ..- attr(*, "order")= int 1
## .. ..- attr(*, "intercept")= int 1
## .. ..- attr(*, "response")= int 1
## .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
## .. ..- attr(*, "predvars")= language list(zeit_bib, anreise)
## .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
## .. .. ..- attr(*, "names")= chr [1:2] "zeit_bib" "anreise"
## $ model :'data.frame': 200 obs. of 2 variables:
## ..$ zeit_bib: num [1:200] 299 278 199 326 259 ...
## ..$ anreise : num [1:200] 7.06 11.34 106.81 24.97 28.11 ...
## ..- attr(*, "terms")=Classes 'terms', 'formula' language zeit_bib ~ anreise
## .. .. ..- attr(*, "variables")= language list(zeit_bib, anreise)
## .. .. ..- attr(*, "factors")= int [1:2, 1] 0 1
## .. .. .. ..- attr(*, "dimnames")=List of 2
## .. .. .. .. ..$ : chr [1:2] "zeit_bib" "anreise"
## .. .. .. .. ..$ : chr "anreise"
## .. .. ..- attr(*, "term.labels")= chr "anreise"
## .. .. ..- attr(*, "order")= int 1
## .. .. ..- attr(*, "intercept")= int 1
## .. .. ..- attr(*, "response")= int 1
## .. .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
## .. .. ..- attr(*, "predvars")= language list(zeit_bib, anreise)
## .. .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
## .. .. .. ..- attr(*, "names")= chr [1:2] "zeit_bib" "anreise"
## - attr(*, "class")= chr "lm"Als Erstes sehen wir uns die Zusammenfassung des Modells an. Die nicht tidy-Form enthält sehr viel Information, die man am Anfang gar nicht braucht. Und sie glänzt mit vielen Signifikanz-Sternchen, die wir am liebsten gleich verbannen würden.
summary(lin_mod)##
## Call:
## lm(formula = zeit_bib ~ anreise, data = befragung)
##
## Residuals:
## Min 1Q Median 3Q Max
## -60.060 -14.063 0.836 15.662 64.151
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 302.09377 2.28190 132.39 <2e-16 ***
## anreise -0.76627 0.05112 -14.99 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 20.85 on 198 degrees of freedom
## Multiple R-squared: 0.5316, Adjusted R-squared: 0.5292
## F-statistic: 224.7 on 1 and 198 DF, p-value: < 2.2e-16Daher empfehle ich die tidy-Form. Wir nutzen die Funktion get_regression_table aus der Bibliothek moderndive, die intern auf die Bibliothek broom zugreift (https://cran.r-project.org/web/packages/broom/vignettes/broom.html). broom hilft, die Ausgabe des linearen Modells in eine tidy-Form zu konvertieren. Die Funktion kable() aus der Bibliothek knitr layoutet die Tabelle.
get_regression_table(lin_mod) %>% kable()| term | estimate | std_error | statistic | p_value | lower_ci | upper_ci |
|---|---|---|---|---|---|---|
| intercept | 302.094 | 2.282 | 132.387 | 0 | 297.594 | 306.594 |
| anreise | -0.766 | 0.051 | -14.990 | 0 | -0.867 | -0.665 |
Sie sehen in der ersten Spalte (Intercept) und anreise. Das sind der \(y\)-Achsenabschnitt \(\beta_0\) und die Steigung \(\beta_1\) des Modells. Das heißt, unser Modell lautet ausgeschrieben:
\[\widehat{\text{zeit_bib}_i} = 302.094 - 0.766 \cdot \text{anreise_i}\] Der Index \(i\) steht hier für die unterschiedlichen Studierenden, denn jede(r) hat natürlich eine eigene Anreise- und Arbeitszeit in der Bibliothek. Wir lernen also, dass mit steigender Anreisezeit, die Arbeitszeit in der Bibliothek sinkt. Und zwar können wir es sogar noch genauer sagen: mit jeder zusätzlichen Minute Anreisezeit, sinkt die Arbeitszeit in der Bibliothek um 0.766 Minuten. Auf die übrigen Spalten kommen wir später zu sprechen.
Welche Werte hat das Modell berechnet? Diese nennt man angepasste Werte (fitted) und man kann sie mit der Funktion fitted() abfragen. Wir sehen uns nur die ersten Einträge an.
## 1 2 3 4 5 6
## 296.6866 293.4026 220.2491 282.9618 280.5521 284.0451Wir würden gerne diese angepassten Werte mit den echten gemessenen Werten, nämlich der tatsächlichen Arbeitszeit in der Bibliothek, vergleichen. Dafür fügen wir die gemessenen und die angepassten Werte in einem tibble zusammen. Wir erstellen eine neue Spalte mit angepassten Werten und den Residuen, d.h. den Differenzen zwischen den gemessenen und den angepassten Werten.
Nun können wir die Werte gegeneinander plotten und uns die Residuen ansehen. Diese sind als graue vertikale Linien zwischen den gemessenen und den angepassten Werten dargestellt. Die angepassten Werte liegen alle auf einer Geraden, das ist ja die Quintessenz eines linearen Modells. Zu jedem gemessenen Wert gibt es einen angepassten, modellierten Wert auf der Geraden. Das geom geom_abline zeichnet unsere Gerade.
ggplot(model_res, aes(x = anreise, y = zeit_bib)) +
geom_segment(aes(xend = anreise, yend = fitted, lty = 'Residuen'), alpha = 0.2) +
geom_abline(intercept = coef(lin_mod)[1], slope = coef(lin_mod)[2], color = "lightblue") +
geom_point(aes(col = 'observed')) +
geom_point(aes(y = fitted, col = 'fitted'), shape = 1, size = 2) +
labs(x = 'Anreisezeit (min)', y = 'Arbeitszeit in der Bibliothek (min)') +
scale_color_manual(name = '', values = c(observed = 'black', fitted = 'blue'), breaks = c('observed', 'fitted'), label = c('Gemessene Werte', 'Angepasste Werte')) +
scale_linetype_manual(name = '', values = ('Residuen' = 'solid')) +
theme(legend.position = 'bottom')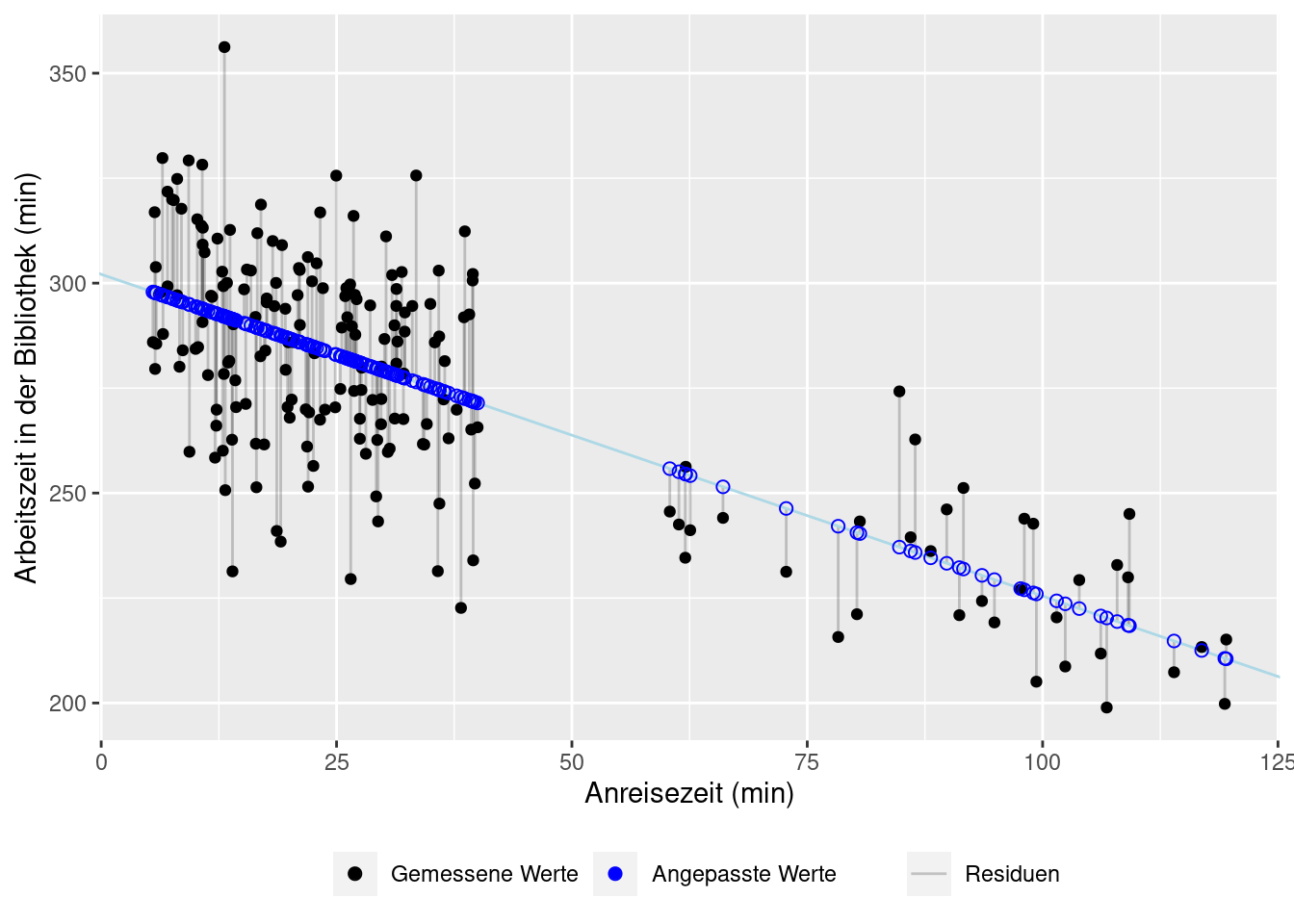
11.4.3 Modellannahmen überprüfen
Bei der linearen Regression nehmen wir an, dass der Zusammenhang zwischen der Zielvariablen und dem Prädiktor linear ist. Das können wir an der oberen Grafik bereits erkennen. Weiterhin nehmen wir an, dass die Residuen im Mittel um die Null schwanken und homoskedastisch sind, d.h. ihre Varianz ist gleich. Diese Annahmen müssen wir überprüfen, bevor es ans Interpretieren der Modellparameter geht. Das macht man hauptsächlich grafisch. Wir plotten die Residuen gegen die angepassten Werte.
ggplot(data = model_res, aes(x = fitted, y = residuals)) +
geom_point() +
geom_hline(yintercept=0, col = 'red') +
labs(x = 'Angepasste Werte', y = 'Residuen')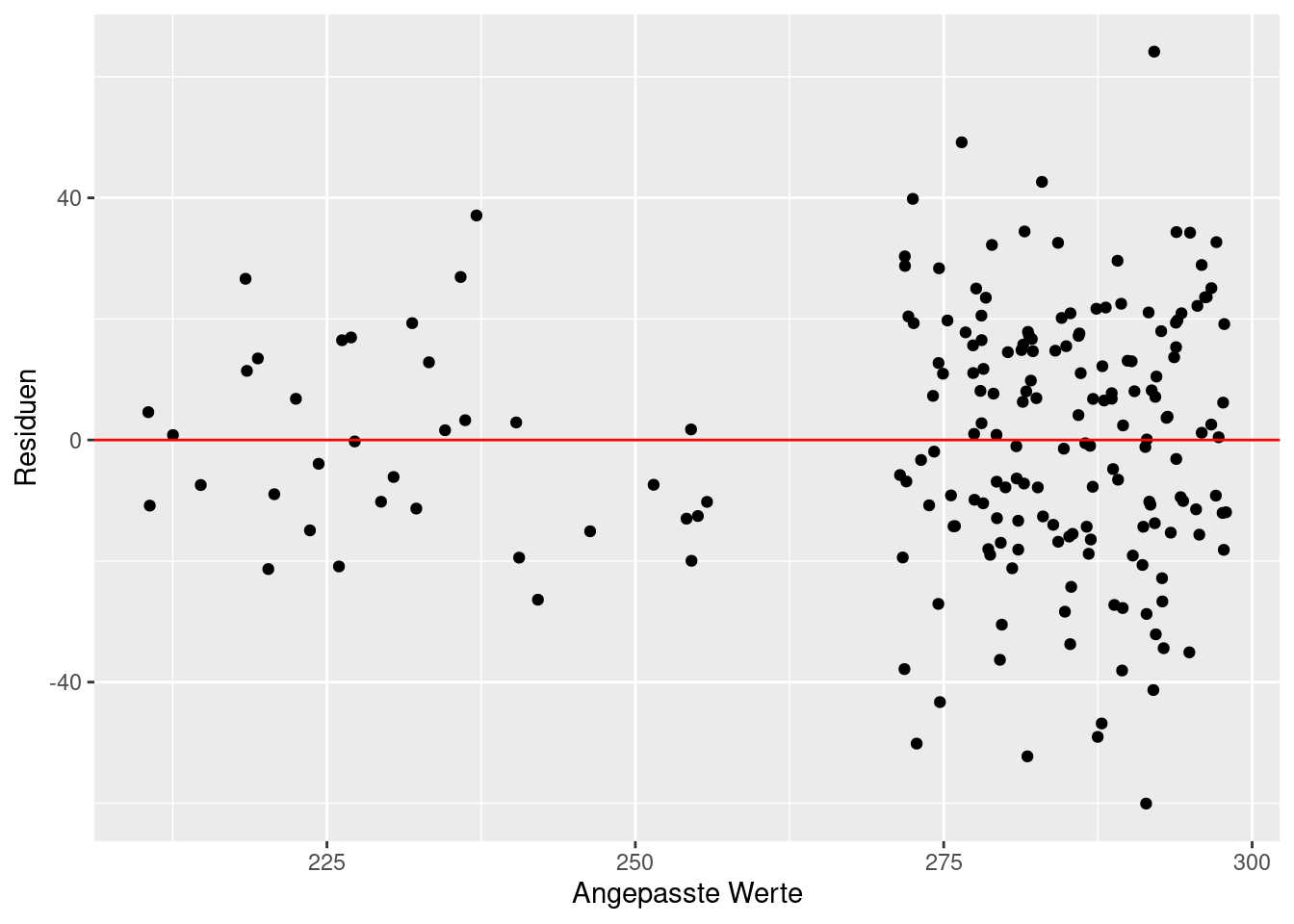
Diese Darstellung der Residuen gegen angepasste Werte nennt man Residualplot. Darin können wir erkennen, dass unsere Residuen um die Null schwanken. Die erste Annahme ist also schon einmal erfüllt. Die Homoskedastizität ist nicht ganz erfüllt. Bei größeren angepassten Werten scheinen die Residuen stärker zu schwanken. Allerdings gibt es nur sehr wenige Werte < 250 Minuten. Daher ist es schwierig, daraus eine echte Heteroskedastizität abzuleiten. Wichtig ist, dass wir keine systematische Zunahme oder Abnahme der Variabilität beobachten und auch keine sonstigen Muster in den Residuen. Die zweite Modellannahme können wir auch als erfüllt abhaken. Wir können plausibel davon ausgehen, dass die Residuen unabhängig sind. Denn wir haben weder eine Zeitreihe gemessen, noch Leute mehrfach befragt.
Die Zusammenfassung des linearen Modells bietet noch weiter Informationen.
get_regression_table(lin_mod) %>% kable()| term | estimate | std_error | statistic | p_value | lower_ci | upper_ci |
|---|---|---|---|---|---|---|
| intercept | 302.094 | 2.282 | 132.387 | 0 | 297.594 | 306.594 |
| anreise | -0.766 | 0.051 | -14.990 | 0 | -0.867 | -0.665 |
Hier gibt es noch die Spalten
-
std_error: Standardfehler der Schätzung des jeweiligen Modellparameters (intercept oder anreise) -
statistics: Wert der \(t\)-Statistik für einen Hypothesentest, der überfüft, ob der jeweilige Modellparameter Null ist. Die Nullhypothese lautet \(\beta_0 = 0\) für den \(y\)-Achsenabschnitt bzw. \(\beta_1 = 0\) für die Steigung. Die Alternativhypothese lautet, dass der jeweilige Modellparameter ungleich Null ist. -
p-value: p-Wert des Hypothesentests -
lower_ci,upper_ci: unterer und oberer Wert des Konfidenzintervalls (Standardeinstellung 95%)
Für die Berechnung des Standardfehlers, des Hypothesentests und der Konfidenzintervalle wird, zusätzlich zu den oben genannten Annahmen, vorausgesetzt, dass die Residuen normalverteilt sind. Nur wenn sie es tatsächlich sind, sind diese Berechnungen und der Hypothesentest korrekt, sonst möglicherweise nicht. Deswegen müssen wir, bevor wir diese Spalten interpretieren, überprüfen, ob die Residuen normalverteilt sind. Das machen wir mit einem QQ-Plot. Sie dürfen auch noch einen formalen shapiro.test() machen, wenn Sie möchten.
ggplot(model_res, aes(sample = residuals)) +
stat_qq() +
stat_qq_line(col = 'blue') +
labs(x = 'Quantile aus der Normalverteilung',
y = 'Qunatile der Daten')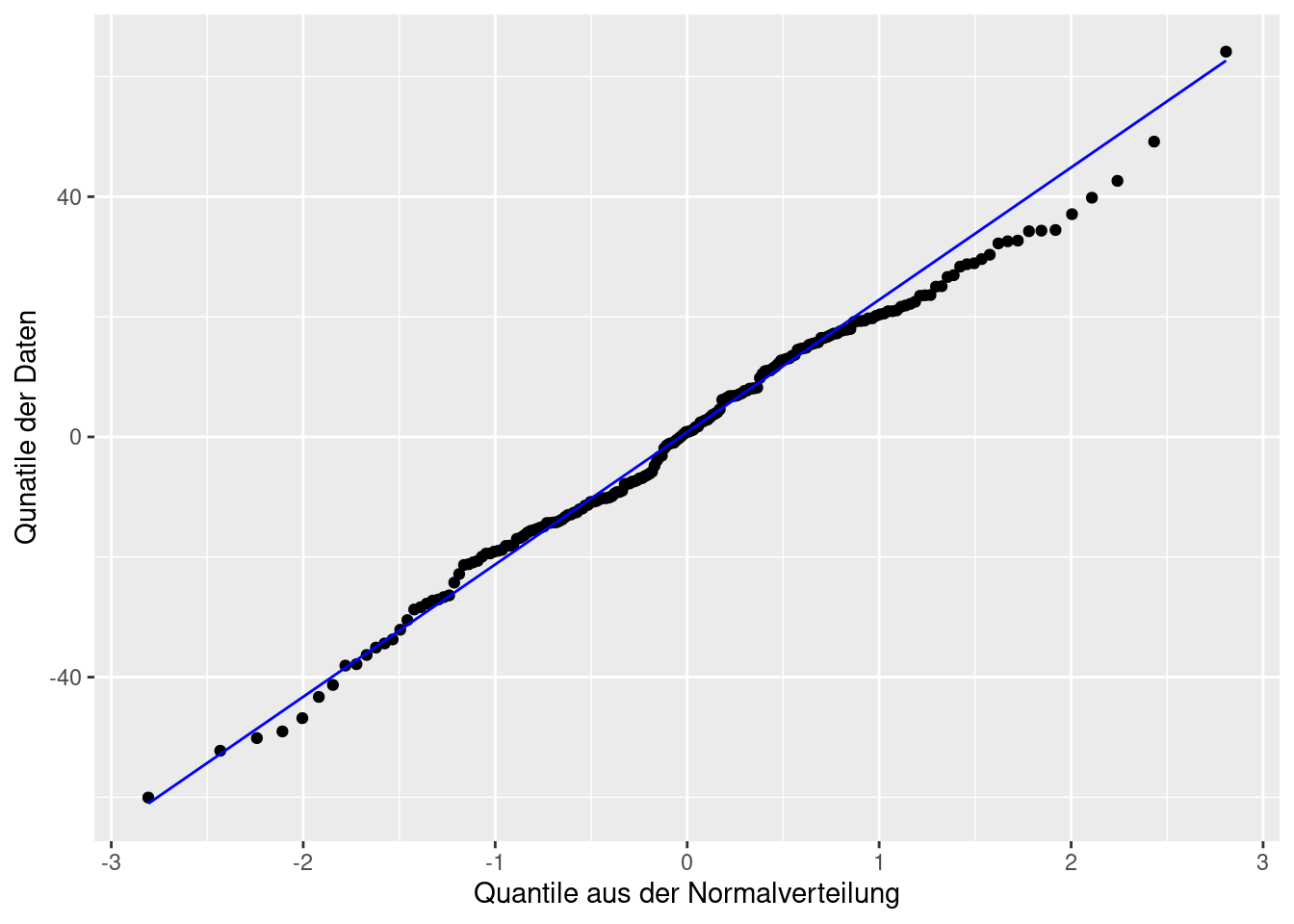
Wenn die Residuen normalverteilt sind, dann liegen sie nahe der Geraden im QQ-Plot. Das ist hier der Fall. Die Annahme der Normalverteilung der Residuen ist also erfüllt und wir dürfen den Standardfehler, den p-Wert und die Konfidenzintervalle interpretieren.
11.4.4 Modell interpretieren
In unserem fiktiven Datensatz nimmt die Arbeitszeit in der Bibliothek mit der Anreisezeit ab. Wir haben bereits die Schätzungen des \(y\)-Achsenabschnitts (intercept) und der Steigung (anreise) interpretiert. Jetzt können wir zusätzlich sagen, wie gut wir geschätzt haben. Der \(y\)-Achsenabschnitt gibt die Anreisezeit in der Bibliothek an, wenn die Anreisezeit Null wäre. Das ist zwar die korrekte Interpretation, aber eine Extrapolation außerhalb unseres Messbereichs der Anreisezeit. Daher sollte man den \(y\)-Achsenabschnitt nicht überinterpretieren. Er ist erst einmal ein Modellparameter, der gut geschätzt wurde, mit einem Konfidenzintervall von [297.594, 306.594]. Ob die Studierenden tatsächlich diese Zeit in der Bibliothek verbringen würden, wenn sie gewissermaßen auf dem Campus wohnen würden, ist eine Spekulation.
Einfacher und sinnvoller ist die Interpretation der Steigung. Ihr Konfidenzintervall lautet [-0.867, -0.665]. Es ist eine gute Schätzung, da das Konfidenzintervall schmal ist. Pro zusätzlicher Anreiseminute sinkt die Arbeitszeit in der Bibliothek um einen Wert in diesem Konfidenzintervall.
Die Hypothesentests können Sie interpretieren, wie gewohnt, müssen Sie aber nicht. Wie in den vorherigen Kapiteln erwähnt, kann man auf den Begriff signifikant getrost verzichten. Die Schätzung der Parameter und deren Konfidenzintervalle bringt sehr viel mehr Information.
Zum Schluss noch die wichtigsten Take-Home Messages.- Regression beinhaltet eine große Familie an Modellen.
- Lineare Regression: linearer Einfluss der Kovariablen auf \(y\).
- Annahmen: Residuen \(\varepsilon_i\) sind iid mit \[\mathrm{E}(\varepsilon_i) = 0, \qquad \mathrm{Var}(\varepsilon_i)=\sigma^2.\]
- Normalregression zusätzlich: \(\varepsilon_i \sim N(0,\sigma^2)\).
- Überprüfung der Annahmen (vor allem) grafisch.
- Konfidenzintervalle und Hypothesentests der Normalregression dürfen nur dann interpretiert werden, wenn die Annahmen erfüllt sind.